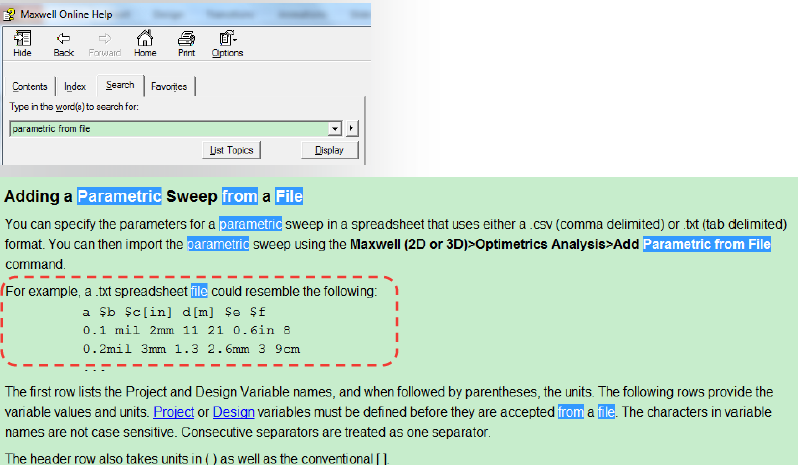
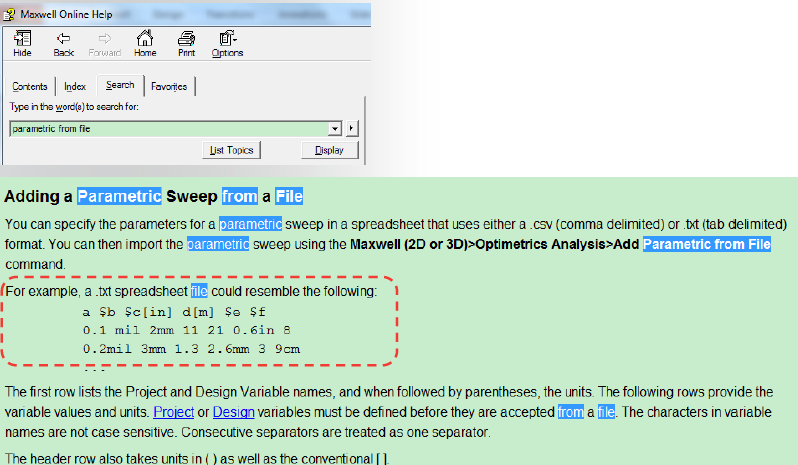
Starting in the 1950s, automotive and aerospace companies purchased significant amounts of computer hardware. A number of the companies developed their own CAD/CAM programs to support the complexities and scale of their product development process. Not only were there few commercial CAD/CAM companies, but industrial companies also wanted to protect their intellectual property.
CAD/CAM programs supported drafting, 3-D surface modeling, numerical control (NC) programming, and/or engineering analysis. Drafting let users produce engineering drawings that documented designs and contained fabrication and assembly instructions. Some industrial companies, especially in the automotive and aerospace sectors, pushed the CAD envelope into 3-D surface modeling because surfaces define the external skins that drive automotive style and aerospace aerodynamics. Using the geometry CAD produced, CAM programs generated NC instructions for a new class of highly accurate machine tools. Finally, the geometry was essential input to complex engineering analysis programs (such as stress and aerodynamics).
This article begins with a general background and overview of the drafting, engineering, and manufacturing requirements in the automotive and aerospace industries. It then describes some of the technical differences between interactive CAD programs and other scientific and engineering programs in terms of performance, scale, and integration. The article then provides an overview of some of the program functions needed and why most of them were not available on a commercial basis.
This general picture is then followed by a more detailed discussion of CAD/CAM program examples from the two industries up through the mid-1980s. The automotive industry is covered first, with detailed examples from General Motors (GM), Ford, and Renault/Citroën. A similar discussion of the aerospace industry follows, with a focus on Lockheed, Northrop, McDonnell Douglas, Dassault Aviation, and Matra Datavision.
The article ends with a discussion of why and how these companies led the way in high-performance, large-scale, complex 3-D surface and NC programs. By contrast, early commercial CAD/CAM software companies focused on building programs that produced engineering drawings. In some cases, industrial companies purchased commercial programs to produce engineering drawings but relied on internal development for surface design and NC programming.
BACKGROUND
Like most forms of computing technology, CAD systems have evolved significantly. Some advances have been driven by computing technology itself, such as graphics processing units, personal computers, and cloud computing. Other have been driven by brilliant people developing and improving algorithms (such as finite elements for 3D stress analysis and nonuniform rational b-splines). Importantly, industrial companies realized that productivity improvements over manual techniques were possible using interactive graphics.
Automotive and aerospace companies have found benefits in developing and using highly interactive, computer-graphics-based CAD/CAM programs since the late 1950s. Computing helped automotive and aerospace companies move into the world of automated milling and machining with NC systems (CAM), analyzing smooth surfaces to define aerodynamically efficient and aesthetically pleasing external surfaces [computer-aided engineering (CAE)], and producing engineering drawings (CAD). Starting in the 1980s, other industries, such as shipbuilding, architecture, petrochemical plants, and manufacturing/assembly plants, adopted CAD/CAM methods more slowly.
Production-level automotive and aerospace CAD/CAM programs had features commercial companies introduced later. Early commercial offerings, as documented in David Weisberg’s excellent book [28], focused on generating engineering drawings. A few early industrial systems, such as Lockheed’s CADAM system, which became successful commercially [28, pp. 13-1–13-7], addressed engineering drawing, while other companies (such as Boeing and Ford) used commercial drafting systems.
Systems developed by industrial companies included not only 2-D engineering drawings but also CAM, engineering analysis, and 3-D surface design. By contrast, early commercial systems concentrated on producing 2-D engineering drawings. Daniel Cardoso Llach’s article [9] in this issue discusses how the 1950s CAM push to improve input definition for numerically controlled milling machines influenced some of the earliest CAD developments. Engineering analysis and surface-definition capabilities are discussed later in this article and the article by Kasik et al. [17].
Industrial and commercial systems differed for multiple reasons. First, CAD/CAM programs produce the complex, digital geometric representations and annotations needed to design, analyze, manufacture, and assemble products. Industrial companies wrote their own programs to protect their proprietary methods. Second, industrial companies chose to directly hire mathematicians, engineers, and programmers to build customized programs for 3-D surface design and engineering analysis. The programs reflected internal company practices and did not need to be as general as commercial offerings. A significant amount of the computer graphics techniques and mathematics implemented in industrial CAD/CAM programs still exist in today’s commercial offerings. Third, industrial companies were able to purchase mainframe computing. Mainframe performance was especially necessary for surface design and engineering analysis.
OVERVIEW
CAD/CAM programs produce two types of basic data. First, both automotive and aerospace require 3-D geometry to define their products. Second, they require text and 2-D/3-D geometry as input for engineering analysis (CAE) and instructions (such as finish, tolerances, and dimensions) for manufacturing and assembly. (Engineering analysis and CAE systems are beyond the scope of this article.)
Because the documentation medium is something flat (on paper, a computer screen, or microfilm), companies have long used 2-D engineering drawing techniques to represent 3-D geometry. The drawings represent 3-D objects as a collection of views (see Figure 1). Even if the CAD/CAM program defines geometry using 3-D coordinates, rendering techniques (such as shading, perspective, and dynamic rotation) are required to help the user understand the 3-D geometry on flat screens (see Figure 2).
FIGURE 1. Typical engineering drawing. (Source: https://pixabay.com/vectors/car-vehicle-draw-automobile-motot-34762/; used with permission.)
FIGURE 2. Annotated 3-D object. (Source: D. Kasik; used with permission.)
In short, CAD/CAM programs implement the necessary techniques to define, modify, and communicate the 2-D/3-D geometry and text needed to build complex products.
My Boeing job gave me a broad view of both commercial and industrial systems. As chief technical architect for Boeing’s internally developed CAD system [16], I was invited to numerous presentations from vendors and competitors and became acquainted with their internal details. Boeing CAD/CAM research and development work started in the late 1950s and ended in the late 1990s.
Academic systems are not included in this article because the most significant production program development work was being done by commercial CAD software companies and industrial companies. A number of academic research projects inspired CAD/CAM development nonetheless. The Massachusetts Institute of Technology [28, pp. 3-1–3-25] provided excellent late-1950s and early-1960s results focused on interactively generating 2-D geometry [24], 3-D geometry [15], and NC machine programming [23]. Although there were some academic contributions to solid modeling [27], [25], solids did not play a significant modeling role until Boeing used CATIA V3 and CATIA V4 to define the 777 with solids [21].
When assessing automotive and aerospace CAD programs, it is necessary to understand not only the data but also the user community:
those with technical expertise in one or more scientific, engineering, or manufacturing fields
specialists with interactive CAD systems build 2-D engineering drawings or 3-D models based on specifications from technical experts.
programming skills and are willing to write their own software to solve problems not addressed to their satisfaction in commercial software.
The models and text guide the activities of downstream engineering, fabrication, assembly, and maintenance staff. Making the downstream more productive was a prime motivator for the development of early CAD programs. CAM programs started in the mid-1950s because NC machines required very lengthy programs that required part geometry and manufacturing instructions to fabricate individual parts [2]. Generating the geometry for NC programs led to the development of tools to make defining the geometry easier. Engineering programs (such as computational fluid dynamics and finite-element analysis) also relied on geometry that defined external surfaces for aerodynamic analysis, more detailed part forms for structural analysis, and many others.
CAD/CAM PROGRAM CHARACTERISTICS
On a technical level, interactive CAD/CAM programs differ from other scientific/engineering programs and transaction-oriented business systems because of the greater need for performance, scale, and integration. However, CAD/CAM programs and their users did not initially levy specific demands on processor speed, network speed, memory size, and data storage capacity. Instead, users tended to start with whatever technical facilities they could access and then later demanded more processor power, network bandwidth, memory, and data storage.
Performance Requirements
CAD/CAM interactive drafting and design performance must be close to real time to allow users to manipulate geometry (either 2-D or 3-D) efficiently and comfortably. Immediate response (measured as 0.5 seconds or less) [28, pp. 13-1–13-7] for simple operations makes the CAD/CAM program feel like it is responding in real time. Simple operations include sketching a line and rotating, moving, and zooming 3-D models.
By contrast, many other scientific/engineering programs are heavily compute-bound and can generally be run as batch programs. Even when able to be run interactively, users understand how complex the algorithms are and do not expect immediate results. Hence, the necessity for real-time interaction is relaxed.
Most interactive, transaction-oriented business systems do not require near-real-time interactive performance. They often feature form interfaces that require a person to fill out multiple fields prior to processing. Interaction must be fast enough to allow quick navigation from one text field to another. Once input is completed, the user starts transactions processed by a reliable database system and expects some delay.
The real-time interaction aspect of CAD/CAM programs meant that their implementation differed significantly from other types of online programs. Getting acceptable performance for CAD stressed interactive devices, operating systems and programming languages; data storage methods; and computing/network hardware.
Other forms of scientific computing generate or measure vast amounts of data, as in computational fluid dynamics or astronomy. When a person produces a CAD drawing or model, it is most often part of a larger collection of parts, subassemblies, and assemblies that ultimately define the entire product. A complex product, such as a commercial airplane or a building, requires thousands of drawings, hundreds of thousands of unique parts, and millions of individual parts. A configuration management system rather than a CAD system defines and controls interpart relationships and versions. (Configuration management systems are beyond the scope of this article.) The system must be able to handle all of the original data as versions evolve in addition to the data generated by CAE/CAM processes. All versions are stored to document design decisions and evolution.
The thousands of people involved in designing, analyzing, building, and maintaining a complex product put significant stress on the supporting software and hardware. It is critical for the software to keep track and organize all of the parts, drawings, analyses, and manufacturing plans. Tracking and organizing generally required centralized computing resources (yesterday’s mainframes and today’s cloud). Tracking and organizing CAD data on centralized mainframes was difficult enough. The problem got worse as personal computers started having enough computing power and networking resources to move design to a distributed computing environment. Although tracking and organizing mainframe-based data were difficult, and distributed work relied on detailed centralized tracking and organizing, making sure that a user was working on the latest version added complexity.
Scale: Product Complexity and Longevity
The problem of scale stresses computer systems across both size and time. Then, as computer performance improves, users tend to push the limits by attacking more complex problems, producing more design and simulation iterations, generating more numerous and more detailed models, and so on. For example, when Boeing developed the 777 during the late 1980s and early 1990s, each airplane was represented by a collection of models that contained about 300 million polygons. The fourth version of the Dassault Systèmes CATIA CAD system (CATIA V4) was the primary modeling tool. When the 787 started in 2004, the geometric models developed using CATIA V5 required more than 1 billion polygons. Although not necessarily as large in terms of absolute amounts of storage consumed as business systems, geometry data are structurally complex (with both intrapart and interpart relationships) and contain mostly floating-point values (for example, results of algorithms only come close to zero).
Scale is also measured in calendar time. CAD programs generate geometry and documentation data that represent products that could be in use for decades (such as aircraft and military aircraft) or more (such as power generators). CAD/CAM programs tend to have a shorter half-life than the product definition data they produce. This puts significant stress on data compatibility across vendors or across software versions from the same vendor. Different vendors’ implementations of the same type of entity could all too easily result in translation errors. New versions of a single vendor’s product could also result in translation errors.
Data Integration
CAD/CAM program integration has different variations [18]. Effective, active data integration allows different programs to read and potentially write geometry data directly without translation. For example, a finite-element analysis program requires geometry from which it builds a mesh of elements. Many analysis programs (such as NASTRAN) have been in existence for decades and still do not have direct access to CAD geometry models.
Having full data integration across all CAD/CAM/CAE programs is a complex and fragile endeavor that remains a challenge for multiple reasons. Different groups developed the programs and use different internal representational that require translation. For example, CAD-generated geometry must be translated into the nodes and elements that finite-element codes can process. Similarly, different organizations use different brands of CAD/CAM/CAE programs that also require translation. For example, Boeing used two different CAD systems (Computervision for the 757 and Gerber for the 767) that forced the company to develop its own translator.
The translation of geometric data has proven to be nearly as challenging as translating natural language. Programs often have unique data entities, different algorithms for the same function, and even different hardware floating-point representations. The differences mean that 100% accurate and precise translation among systems has yet to be realized.
INTERNAL AUTOMOTIVE AND AEROSPACE PROGRAM DEVELOPMENT
Three factors drove CAD/CAM adoption in the aerospace and automotive industries. First, companies observed that engineering drawing preparation was time-consuming for both an initial release and subsequent modifications. Interactive graphics obviated the need for drafting tables, drafting tools, and erasers. Drafters could generate and modify engineering drawings more quickly. Large plotters on paper or mylar for certification agencies, such as the U.S. Federal Aviation Authority, for approval. Second, engineering analysis showed real promise in terms of virtually analyzing engineering characteristics, such as aerodynamics, structural integrity, and weight. Accurate geometry, especially external surface definitions, was required. Third, NC machines gained popularity and required efficient methods to create the geometry of individual parts.
Many automotive and aerospace companies developed their own programs. Unlike the early commercial CAD/CAM companies, which often relied on minicomputers, automotive and aerospace companies had enough mainframe resources to support a large user community and large amounts of data. A single mainframe could be upgraded to support, test, and even hundreds of CAD/CAM users and provide acceptable interactive performance. In addition, aerospace and automotive companies hired the mathematical and programming talent needed to build CAD/CAM programs. The programs were tuned to internal corporate drafting standards, manufacturing, and surface-modeling techniques.
Commercial CAD software systems were able to penetrate a few large companies in the early days. For example, Boeing used them for 757 and 767 engineering drawings. However, it was more common for large aerospace and automotive companies to develop their own systems to give themselves a competitive advantage in surface modeling and NC programming. A few other large design and build companies in the shipbuilding, architecture, industrial design, process plant, and factory design industries also developed or used early CAD systems, like Fluor [20] and GE [2], but they were the exceptions. Automotive and aerospace led the way, but, in many cases, surface modeling and NC programming were the prime focus. Engineering drawing programs were developed primarily to save documentation labor.
Both commercial software companies and industrial companies developed dozens of CAD/CAM programs that had significant functional overlap. As is the case with other product classes, many competitors initially emerged. However, market evolution saw the many gradually coalesce into a few large players. The CAD/CAM business was no different. Today, a few large players (Autodesk, Dassault Systèmes, Parametric Technology, and Siemens) acquired competitors or forced them into bankruptcy and now dominate the market [28, pp. 8-1–8-51, 13-1–13-7, and 16-1–16-48, and 19-1–19-38].
The internal industrial programs stayed in production through the mid- to late 1980s. Commercial software companies started adding functions for 3-D solid and surface modeling and advanced NC programming. The commercial companies were able to spread development and maintenance costs over multiple clients, and industrial companies realized that commercial systems could provide cost savings.
The power of personal computers based on raster graphics devices also started matching and even exceeding minicomputer and workstation performance. Personal computers, which were much cheaper and offered another cost-savings opportunity, contributed to the demise of mainframe-based systems.
AUTOMOTIVE INDUSTRY
Companies like General Motors [19] and Renault [4] had strong research and development organizations and started recognizing CAD’s benefits in the late 1950s.
FIGURE 3. Coordinate measuring machine. (Source: https://www.foxvalleymetrology.com/products/metrology-systems/coordinate-measuring-machines/wenzel-r-series-horizontal-arm-coordinate-measuring-machines/wenzel-raplus-horizontal-arm-coordinate-measuring-machine/; used with permission.)
Automotive surfaces are often defined using full-scale clay models (see Figure 3). While manual sculpting of new car body designs in clay was hard enough, manually transferring computer-pressable surfaces to support design, engineering, and manufacturing was even harder. Companies still use full-size coordinate measuring machines and numerical surface-fitting algorithms to do so.
The automotive industry especially cares about how a vehicle looks to a potential buyer. Mathematicians like Steve Coons (Massachusetts Institute of Technology, Syracuse, and Ford), Bill Gordon (GM and Syracuse), and Pierre Bézier (Renault) solved complex computational geometry problems both as academics and as employees. Their solutions became the basis for substantial improvements in surface modeling. The methods for defining surfaces, true 3-D objects, varied from company to company. For example, General Motors used full-scale coordinate measuring machines that capture height along the width and the length of a full-scale clay model of a proposed automobile. Bill Gordon’s surface algorithms accounted for height differences in the width and length measurements.
GM
GM started its CAD developments in the late 1950s [19]. The staff at GM Research (GMR) worked with IBM to develop time-sharing and graphics capabilities that were responsive enough to support interactive design. The original computer used was an IBM 704 (upgraded to a 7090 and then a 7094) running a Fortran language compiler. The program itself was called Design Augmented by Computers (DAC-1).
It not only did DAC-1 provide body-styling assistance, but it also forced the IBM–GM team to develop an early time-sharing strategy (the Trap Control System) in 1961. Time sharing itself was in its infancy in the 1960s and generally supported alphanumeric character terminals connected at low speeds (110 or 300 bits per second). Supporting interactive performance required higher bit rates and put more pressure on the operating system. Earlier computers, such as Whirlwind, that supported graphics and light-pen interactive devices were dedicated to a single user.
IBM and GM formed a joint development project to develop a light-pen-driven interactive device to meet GM’s DAC-1 requirements. Even the choice of programming language was scrutinized. The Fortran compiler proved to be too slow, so DAC-1 moved to NOMAD, a customized version of the University of Michigan’s Michigan Algorithm Decoder compiler, in 1961–1962 [19].
Patrick Hanratty and Don Beque worked on the CAM systems that dealt with stamping the designs produced by DAC-1 between 1961 and 1964. Hanratty left GM in 1965 and went to a West Coast company, where he developed his design software. He later took his work and formed an independent company [2], [38, pp. 15-1–15-20].
DAC-1 was formally moved from the GMR to GM operating division in 1967, but they did not use the GM CAD system development. Two different surface-modeling packages, Fisher Body and CADANCE, appeared in the 1970s. Each ran on IBM 360/370 machines using the PL/1 programming language. Most users had access to IBM 2250/3250 graphics terminals [17]. Some GM divisions reported between 50 and 100 GM devices with DEC GT40 vector graphics terminals hooked up to a PDP 11/45. The 11/05 handled communication to and from the mainframe. In the late 1970s, Fisher Body and CADANCE were merged into GM’s Corporate Graphics System (CGS). The systems were based on GM proprietary surface geometry algorithms. Gordon surfaces [13] were particularly useful when fitting surfaces to scans of data collected from automobile clay body models.
GM developed its own mainframe-based solid-modeling system, GMSolid [7], in the early 1980s that was eventually integrated into CGS. GMSolid used both constructive (i.e., users used solid primitives, like spheres, cylinders, and cones) and boundary representations (i.e., solid faces contained arbitrary surfaces).
Ford
Ford developed a minicomputer-based 3-D system for multiple programs in the mid- to late 1970s. The Ford Computer Graphics System [6] used a Lundy HyperGraf refresh graphics terminal connected to a Control Data 18-10 M minicomputer. Ford modified the operating system to maximize performance. There was one terminal per minicomputer.
The programs supported product design with the Product Design Graphics System to define an auto body using Coons [12] or Overhauser [8] surfaces. Other functions included a printed circuit board design, plant layout, die/tool element modeling, and NC. Ford used commercial CAD systems, such as Computervision and Gerber IDS, for drafting and design functions throughout its powertrain (engine, axle, transmission, and chassis). Ford used different minicomputer brands and graphics terminals for different programs. Computervision ran on its own proprietary minicomputer and a Tektronix direct-view storage tube; Gerber IDS ran on an HP 21MX and Tektronix terminal; and the printed circuit board design program ran on a Prime 400 minicomputer and Vector General refresh graphics terminals.
Even though Ford worked in a distributed minicomputer-based (rather than mainframe-based) environment, the company used centralized servers to store, retrieve, and distribute its design files worldwide.
Renault and Citroën
Pierre Bézier popularized and implemented the curve definitions for defining the smooth curves needed for auto bodies [10] developed by Paul de Casteljau (a Citroën employee) in 1959. Bézier developed the nodes and control handles needed to represent and interactively manipulate Bézier curves via interactive graphics. He was responsible for the development of Renault’s UNISURF system [5] for auto body and tool design. System development began in 1968 and went into production in 1975 on IBM 360 mainframes.
Citroën developed two of its own systems (SPAC and SADUSCA) in parallel with Renault [30]. The systems were also based on de Casteljau’s work and ran on IBM 360 and 370 series computers and IBM 2250 graphics terminals.
AEROSPACE INDUSTRY
In the aerospace CAD/CAM world, companies started defining aerodynamically friendly surfaces shortly before human-powered flight at Kitty Hawk. The National Advisory Committee for Aeronautics (NACA) defined, tested, and published families of airfoils [5] in the late 1920s and 1930s. The idea was to assist aircraft development by predefining the aerodynamic characteristics of wing cross sections (see Figure 4).
FIGURE 4. Sample NACA airfoils. (Source: Summary of Airfoil Data, NACA Report 824, NACA, 1945; used with permission.)
Aerospace engineers must design surfaces that balance aerodynamic performance, structural integrity, weight, manufacturability, fuel efficiency, and other parameters. Industrial aerospace CAD systems adopted 3-D surface-definition technology that was consistent with their company surface-lofting practices and could produce surfaces that could be modified relatively easily, represented conics precisely, and exhibited C2 continuity. (C2 means continuous in the second derivative, an advantage when doing aerodynamic analysis.)
Aerospace companies tried to use automotive surface-modeling methods, but they did not work particularly well. Automobile companies care more about the attractiveness of smooth surfaces, although aerodynamics has become more important as fuel efficiency demands have increased. Aerospace is based on aerodynamic efficiency, and demands C2 continuity in analysis, which were not handled well with automotive surfaces. The development and implementation of nonuniform rational b-spline surfaces became and remain the preferred aerospace surface-modeling method [26].
Lockheed
Lockheed focused on producing engineering drawings and NC programming, not surface modeling. The goal was to be able to speed up both processes.
Lockheed, California developed computer-aided drafting software internally to run on IBM mainframes and 2250/3250 graphics terminals [28, pp. 13-1–13-7]. Development started in 1965 as “Project Design” to create 2-D engineering drawings quickly. Project Design was rechristened as CADAM in 1972. An acceptable response time was deemed to be 0.5 seconds or less. CADAM operators were often judged by how fast they seemed to be working, even if little was actually happening. Generally, CADAM has a lot of relatively short-duration functions that made operators appear busy.
Project Design drawings were used to drive NC machines as early as 1966. Use of the software spread quickly inside Lockheed, which established a separate business to sell CADAM in 1972. The new business started sending CADAM source code to others in 1974, including IBM Paris, Lockheed Georgia, and Lockheed Missile and Space in Sunnyvale, California. Eventually, IBM started a successful effort to offer CADAM (acquired from Lockheed) to drive mainframe sales.
Additional CAD development occurred at Lockheed Georgia in 1965 [28, pp. 4-3–4-4]. Spearheaded by Sylvan (Chase) Chasen, the software ran on CDC 3300 computers and Digigraphics terminals. The purpose was more to assist in NC program path planning than to create engineering drawings.
Northrop
Northrop military program funding often drove the development of aerospace company systems. Northrop Computer-Aided Design and Northrop Computer-Aided Lofting (NCAD/NCAL) is an excellent example [1]. Northrop based the system design for the mid-1970s B-2 Spirit stealth bomber on NCAD/NCAL. Other Northrop military programs and Northrop subcontractors used NCAD/NCAL for 3-D surface modeling and CADAM for drafting.
Northrop used funds from the B-2 program to develop NCAD/NCAL [14] rather than use similar systems from other contractors. NCAD/NCAL ran on IBM mainframes interconnected with classified networks. Importantly, the mainframes and networks crossed multiple corporate boundaries, including Boeing, Hughes Radar, GE Engines, and Vought. All partners had to use NCAD/NCAL and provide their own IBM mainframes. This approach simplified data integration and transfer issues and resulted in the first military aircraft fully designed on a CAD system. The B-2 program started in the early 1980s, and its first flight occurred 17 July 1989. The airplane is still in service today.
McDonnell Douglas
McDonnell Douglas implemented two distinctly different CAD systems [22]. The first, Computer Aided Design and Drafting (CADD), was developed in 1965 by the McDonnell Aircraft Company. It was initially a 2-D design and drafting system that was extended to 3-D in 1973, integrated with NC software in 1976 and sold commercially beginning in 1977.
McDonnell Douglas Automation (McAuto), the computer services business unit, purchased Unigraphics (UG) from United Computing in 1976. McAuto rewrote and expanded the United Computing system software based on a license to Hanratty’s ADAM software. The first production use of UG occurred at McDonnell Douglas in 1978. Bidirectional data exchange between the two was not completed until 1981 even though both were in production use.
The two systems’ implementations differed substantially. CADD ran on IBM mainframes and its geometry was based on parametric cubic polynomials and evaluators. Graphics support was primarily the IBM 2250, a 2-D-only device. Evans and Sutherland (E&S) [11] sold a number of Multi-Picture Systems (MPSs) as a 2250 alternative. The MPS featured hardware for 3-D transformations, which had the potential to offload the mainframe. E&S modified its controller to allow two terminals to share a single controller through a device called a Watkins box (named after the designer and developer, Gary Watkins). The Watkins box was attached to a small DEC minicomputer, which handled communications to and from the mainframe. This configuration provided enough savings over the 2250/3250 to justify the purchase of dozens of E&S terminals.
UG ran on multiple brands of midrange minicomputers, including DEC PDP and VAX systems as well as the Data General S/250, S/230, and S/200. UG derived its geometry from the ADAM system. Early versions of ADAM relied on canonical forms and special case geometry algorithms. Interactive graphics for UG was provided on Tektronix storage-tube devices.
Dassault Aviation
Dassault Aviation started its journey in computer graphics to help smooth curve and surface data in the late 1960s. In 1974, the company became one of the first licensees of Lockheed’s CADAM software for 2-D drafting.
Designing in 3-D took a different route. In 1976, Dassault Aviation acquired the Renault UNISURF program and its Bézier curve and surface capability to complement CADAM.
CATIA itself started in 1978 as the Computer-Aided Tridimensional Interactive (CATI) system. Francis Bernard [3] gave credit for extending CATI to surface modeling to generate geometry that would be easier to machine, a capability particularly important for wind tunnel models. CATI became CATIA in 1981 when Bernard convinced Dassault Aviation to commercialize the system through the Dassault Systèmes spinout. As both an internal and commercial product, CATIA ran on IBM mainframes with attached IBM 2250/3250 and IBM 5080 graphics terminals. The early underlying geometry forms included Bézier curves and surfaces and grew to include canonical solid definitions and constructive solid geometry operations. Later versions ran on IBM RS/6000s and other Unix-based workstations.
Matra Datavision Euclid
French aerospace company Matra’s Euclid system (not to be confused with the C-Side Subtec Euklid system for NC machining) addressed modeling for fluid flow.
Euclid was a modeler sold by the French startup Datavision in 1979. It was originally developed by Brun and Theron in the Computer Science Laboratory for Mechanics and Engineering Sciences in Orsay, France. Its initial purpose was fluid flow modeling. The French conglomerate Matra, which had aerospace components, bought the controlling interest in Euclid in 1980. Dassault Systèmes purchased the software in 1998.
CONCLUSION
Even though internally developed CAD/CAM programs are unusual today, a number of commercial systems had their roots in early industrial programs. Internally developed programs had direct access to user communities and were able to develop math software that matched company practice. The interactive methods and mathematics influenced other industries, such as electronic games and animated films.
Early commercial CAD/CAM programs were packaged as turnkey systems. Each turnkey system supported only a few concurrent users at relatively slow speeds. Industrial companies, which had to support hundreds and even thousands of users, had the computer power (generally large mainframes), the talent (mathematicians and programmers), and the money to build their own proprietary CAD/CAM programs. By the late 1980s, however, there was not enough of a competitive advantage to continue development and support. At that point, commercial companies had developed enough manufacturing, surface design, and other capabilities that internal development and maintenance were no longer cost efficient.
Industrial companies experienced the requirement firsthand by developing their own CAD/CAM programs. Because of that experience, industrial companies can clearly articulate the problems CAD/CAM programs have with performance, scale, and integration to today’s commercial vendors.
As noted earlier, the basic performance and integration requirements for CAD/CAM programs are essentially the same today as in the early days. Scale adds another zero or two to the left of the decimal point as CAD/CAM data quantities grow.
The mainframes and minicomputers of 1960–1985 were supplanted by workstations that cost significantly less. Workstations were overtaken by the ever-increasing compute power and the ability to network personal computers in the mid-1990s. Computing today has a turn-the-clock-back feel as cloud systems are gaining momentum, and current CAD systems are being delivered via the cloud. As was the case with early mainframes, cloud computing centralizes processing and data resources. Users take advantage of high-performance networks and access cloud systems remotely via lower cost PCs. When CAD software is executed in the cloud, license sharing becomes feasible and software updates occur remotely.
When applied to CAD, cloud computing faces the same scale and performance issues present in the early days with centralized mainframes and minicomputers. Cloud scales well from a raw processing perspective. It is easy to add more processing power, and servers are generally in the same physical location, which decreases data transfer costs. What is hard for cloud computing is satisfying CAD systems’ requirement for near-real-time interactive performance, especially at significant distances. Many cloud services are based in data centers that are tens, hundreds, and even thousands of miles away. Such distances make achieving near-real-time interactive performance difficult. Interactive performance continues to force many CAD/CAM applications to run in a distributed manner. Applications run on a PC near the user, whose data are stored on a file server that is configuration managed. When requested, the data are most often checked out from the server, downloaded to the PC, processed locally, and checked back in.
As AI has become more popular, using it to improve CAD/CAM user productivity is also being pursued. There has been significant research into design optimization and automated documentation production, with limited success to date. Design optimization relies on one or more engineering analyses to tweak the geometry. Not only are multiple runs needed to optimize the geometry, but the suggested optimization can force changes to the geometry (such as folds and tears) that to create useful exploded-view drawings typical in a parts catalog from the raw geometry. This seems to be straightforward because assembly components can be easily moved along an x-, y-, or z-axis. The issue is that an exploded view in a parts catalog shows a disassembly/reassembly sequence. Automated disassembly is a task that has been unsuccessfully researched for decades.
CAD/CAM programs are still evolving with significant amounts of work still needed. The field remains as pertinent and as challenging as it was in the early years.
n5321 | 2025年7月7日 22:25






![Typical data assimilation and uncertainty reduction for the uncertain input loads after collecting strain sensor measurements during operation. Here, σ stands for standard deviation. Loading components are given as a function of a parameter s ∈ [0, 1] that wraps around the outer boundary of the component starting at the center of the far right edge of the component. (Color version online.)](https://asmedc.silverchair-cdn.com/asmedc/content_public/journal/mechanicaldesign/143/9/10.1115_1.4050108/1/m_md_143_9_091707_f003.png?Expires=1753874293&Signature=Pm5DDM0U2MedScs~zDolniPBtcKYw-GXrzQMWGZKDlaL1ohruxRiJDmDno~cB49FHdVLjd8YpyO0apVUpwlTaUauyvm5iibMVML26vzsp-~10T43BOAQkXy9NjK3638eaF2vUTk7IEdg1bhxo48VP~48T69TD-uTr3m9WJrTMbHWkb0zHqE-e4esXCY4bG~4STh7I2LGfOUQrEUk5rvhLYt4sxyb5hSi0sBENkF49FQX8fjob9BJicDZv-O-58v7w0mDDPW63EXR8vSkc97BT1fMLoI9ZNbbdqUK6iSgc4hlbywvllQOn3rR3dHhX4zutQPJ-jYzYMvZT3p3dcH9xw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)