2004年发布的波音公司CFD应用30年。
1973到2004.波音搞了数千亿美金的飞机。30年里,波音的工程师所使用的工具必须具备准确预测和确认飞机的飞行特性的能力。在1973年以前,这些工具由解析近似法、风洞试验和飞行测试组成。但是这三十年里,波音用的CFD。
这篇短文讲的是波音的西雅图采购,开发,应用CFD的情况。
介绍
1973 年,波音商用估计有 100 到 200 次的CFD分析。2002年,超过了2W次。这2W次案例涉及的情况也更为复杂。为什么?原因:
现在人们承认 CFD 具有巨大的价值,并在飞行器设计、分析和支持流程中带来了范式转变;
波音公司的 CFD 工作由强大而有能力的远见卓识者 Paul Rubbert 博士领导,他招募并得到了许多才华横溢的管理人员和技术人员的支持;
CFD 工作非常多样化,涉及算法研究、代码开发、应用和验证研究、流程改进和用户支持;
波音公司开发了广泛的产品线,并得到了许多富有创新精神和严格要求的项目工程师的支持;
计算能力和可负担性提高了三到四个数量级;
学术界和政府中的众多先驱者继续在算法上取得突破;
波音公司和政府中的资金经理不反对承担风险。
The role and value of CFD
工程师的目的:预测和确认飞行特性。方式:解析,风洞测试,飞行测试。新方式CFD—— 用数值算法进行仿真分析。CFD 的价值是它以低成本进行少量模拟就能获得完成设计所需的“理解”。具体说,CFD 可用于“逆向设计”或优化模式,预测优化某些流动特性或收益函数(例如阻力)所需的几何形状变化。可以对实验数据(通常通过在风洞中测试飞行器的缩比模型)进行分析,扩展数据,获取准确的飞机的特性。还可以帮工程师找到设计失效问题的根源。
Effective use of CFD is a key ingredient in the successful design of modern commercial aircraft.
有效运用 CFD 是波音成功设计飞机的一项关键因素
聪明、普遍且谨慎地使用 CFD 是波音产品开发的主要战略。Experience to date at Boeing Commercial Airplanes has shown that CFD has had its greatest effect in the aerodynamic design of the high-speed cruise configuration of a transport aircraft.
经验表明CFD) 在波音的飞机设计中发挥了至关重要的作用。过去 20 年使用 CFD 搞飞机开发波音公司节省了数千万美元。数千万美元好像不菲,但它们只是 CFD 为波音创造的价值的一小部分。大头是使用CFD以后为飞机增加附加值。Value to the airline customer is what sells airplanes!
Value is added to the airplane product by achieving design solutions that are otherwise unreachable during the fast-paced development of a new airplane. Value is added by shortening the design development process. Time to market is critical in the commercial world, particularly when starting after a competitor has committed a similar product to market. Very important in the commercial world is getting it right the first time. No prototypes are built. From first flight to revenue service is frequently less than one year! Any deficiencies discovered during flight test must be rectified sufficiently for government certification and acceptance by the airline customer based on a schedule set years before. Any delays in meeting this schedule may result in substantial penalties and jeopardize future market success. The added value to the airplane product will produce increased sales and may even open up completely new markets. The result is more profit to both the buyer and seller (who does not have to discount the product as much to make the sale). All this translates into greater market share.
商业价值详解见上。
CFD 开发和应用过程
In industry, CFD has no value of its own. The only way CFD can deliver value is for it to affect the product. CFD必须成为产品设计、制造和支持工程流程中不可或缺的一部分 。it must get into the hands of the engineers who execute these processes. 理想
The CFD developers and ‘‘expert’’ users can certainly contribute, but are only a part of the engineering process.
将 CFD 投入“生产”并非易事——这通常是一个耗时多年的过程。
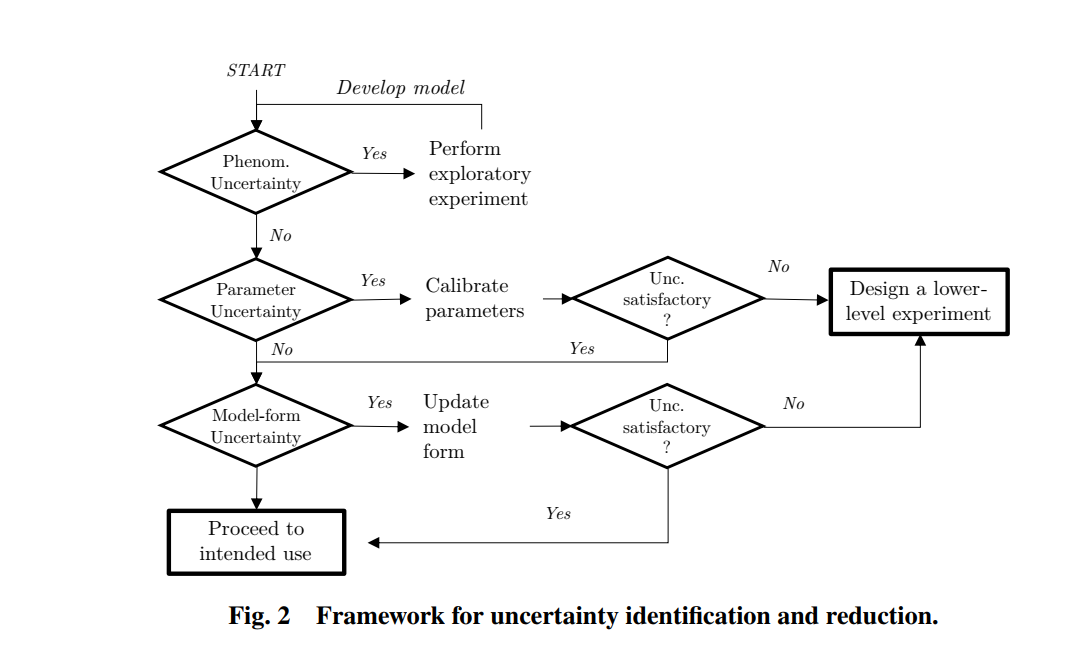
CFD 开发流程分为五个不同的阶段
第一阶段旨在开发使能技术算法,为解决特定问题提供基本方法。
第二阶段是对新计算技术的初步探索、验证和演示。(demo)主要输出是演示代码(可用于计算实验和演示),并结合对实际需求的设想。
第三阶段旨在提供该设想的实质内容,通常需要对第二阶段的代码进行泛化或其他修改(可能是完全重写),并结合前后端界面,以生成用户友好、易于理解且易于维护的软件。They have yet to gain enough confidence to make important, standalone decisions based on the code. That takes time, exposure, and experience.
第四阶段涉及“应用研究”,设计工程师、管理人员和代码开发人员共同努力,研究这项新功能将如何融入并改变气动设计流程。软件落地
第五阶段:成熟的能力。代码通常需要相当长的时间才能达到第五阶段的成熟度
Forrester T. Johnson *, Edward N. Tinoco, N. Jong Yu
Received 1 June 2004; accepted 18 June 2004
Available online 26 February 2005
Abstract
Over the last 30 years, Boeing has developed, manufactured, sold, and supported hundreds of billions of dollars worth of commercial airplanes. During this period, it has been absolutely essential that Boeing aerodynamicists have access to tools that accurately predict and confirm vehicle flight characteristics. Thirty years ago, these tools consisted almost entirely of analytic approximation methods, wind tunnel tests, and flight tests. With the development of increasingly powerful computers, numerical simulations of various approximations to the Navier–Stokes equations began supplementing these tools. Collectively, these numerical simulation methods became known as Computational Fluid Dynamics (CFD). This paper describes the chronology and issues related to the acquisition, development, and use of CFD at Boeing Commercial Airplanes in Seattle. In particular, it describes the evolution of CFD from a curiosity to a full partner with established tools in the design of cost-effective and high-performing commercial transports.
Contents
Introduction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1116
The role and value of CFD . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1117
The CFD development and application process . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1120
Chronology of CFD capability and use . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1124
4.1. Linear potential flow . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1125
4.1.1. First generation methods––early codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1125
4.1.2. First generation methods––TA230 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1126
4.1.3. Second generation linear potential flow method––PANAIR/A502 . . . . . . . . . . . . . . . . . 1128
4.2. Full potential/coupled boundary layer methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1131
4.2.1. A488/A411 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1131
4.2.2. TRANAIR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1132
4.2.3. BLWF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1137
4.3. Euler/coupled boundary layer methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1138
4.4. Navier–Stokes methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1139
4.4.1. Structure grid codes––Zeus TLNS3D/CFL3D, OVERFLOW . . . . . . . . . . . . . . . . . . . . . . 1139
4.4.2. Unstructured grid codes––Fluent, NSU2D/3D, CFD++ . . . . . . . . . . . . . . . . . . . . . . . 1142
4.4.3. Other Navier–Stokes codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1143
4.4.4. Next generation Navier–Stokes codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1143
4.5. Design and optimization methods . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1145
4.5.1. A555, A619 inverse design codes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1145
4.5.2. TRANAIR optimization . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1146
Conclusions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1148
References . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1148
Introduction
In 1973, an estimated 100–200 computer runs simulating flows about vehicles were made at Boeing Commercial Airplanes, Seattle. In 2002, more than 20,000 CFD cases were run to completion. Moreover, these cases involved physics and geometries of far greater complexity. Many factors were responsible for such a dramatic increase: (1) CFD is now acknowledged to provide substantial value and has created a paradigm shift in the vehicle design, analysis, and support processes; (2) the CFD effort at Boeing was led by a strong and capable visionary, Dr. Paul Rubbert, who recruited and was supported by the services of a number of talented managers and technical people; (3) this CFD effort was well diversified, involving algorithm research, code development, application and validation studies, process improvement, and user support; (4) Boeing developed a broad line of products, supported by a number of innovative and demanding project engineers; (5) computing power and affordability improved by three to four orders of magnitude; (6) numerous pioneers in academia and the Government continued to make algorithmic breakthroughs; and (7) there were funding managers in Boeing and the Government who were not averse to taking risks.
It would be impossible to adequately address all these factors in this short paper. Consequently, we will concentrate on issues that were central to the efforts of the authors, who have been members of the CFD Development and Applications groups at Boeing, Seattle for more than 30 years. In Section 2, we describe the role and value of CFD as it has evolved over the last 30 years and as it may possibly evolve in the future. In Section 3, we describe the CFD development and application processes. In Section 4, we lay out a brief history of the codes and methods that were most heavily used at Boeing, Seattle, as well as some of the issues that lay behind their development. In Section 5, we draw some brief conclusions.
Finally, we note that CFD has had a long and distinguished history in many other parts of the Boeing Enterprise. That history would best be related by those intimately involved.
The role and value of CFD
The application of CFD today has revolutionized the process of aerodynamic design. CFD has joined the wind tunnel and flight test as primary tools of the trade [1–4]. Each has its strengths and limitations Because of the tremendous cost involved in flight testing, modern aircraft development must focus instead on the use of CFD and the wind tunnel. The wind tunnel has the advantage of dealing with a ‘‘real’’ fluid and can produce global data over a far greater range of the flight envelope than can CFD. It is best suited for validation and database building within acceptable limits of a development program's cost and schedule. Historically, CFD has been considered unsuited for such as task. However, the wind tunnel typically does not produce data at flight Reynolds number, is subject to significant wall and mounting system corrections, and is not well suited to provide flow details. The strength of CFD is its ability to inexpensively produce a small number of simulations leading to understanding necessary for design. Of great utility in this connection is the fact that CFD can be used in an ‘‘inverse design’’ or optimization mode, predicting the necessary geometry shape changes to optimize certain flow characteristics or a payoff function (e.g., drag). Beyond this, CFD is heavily used to provide corrections for the extrapolation of data acquired experimentally (typically from testing a reduced scale model of the vehicle in a wind tunnel) to conditions that characterize the full-scale flight vehicle. Finally, CFD is used to provide understanding and insight as to the source of undesirable flight characteristics, whether they are observed in subscale model testing or in the full-scale configuration.
Effective use of CFD is a key ingredient in the successful design of modern commercial aircraft. The combined pressures of market competitiveness, dedication to the highest of safety standards, and desire to remain a profitable business enterprise all contribute to make intelligent, extensive, and careful use of CFD a major strategy for product development at Boeing.
Experience to date at Boeing Commercial Airplanes has shown that CFD has had its greatest effect in the aerodynamic design of the high-speed cruise configuration of a transport aircraft. The advances in computing technology over the years have allowed CFD methods to affect the solution of problems of greater and greater relevance to aircraft design, as illustrated in Figs. 1 and 2. Use of these methods allowed a more thorough aerodynamic design earlier in the development process, permitting greater concentration on operational and safety-related features.
The 777, being a new design, allowed designers substantial freedom to exploit the advances in CFD and aerodynamics. High-speed cruise wing design and propulsion/airframe integration consumed the bulk of the CFD applications. Many other features of the aircraft design were influenced by CFD. For example, CFD was instrumental in design of the fuselage. Once the body diameter was settled, CFD was used to design the cab. No further changes were necessary as a result of wind tunnel testing. In fact, the need for wind tunnel testing in future cab design was eliminated. Here, CFD augmented wind tunnel testing for aft body and wing/body fairing shape design. In a similar fashion, CFD augmented wind tunnel testing for the design of the flap support fairings. The wind tunnel was used to assess the resulting drag characteristics. CFD was used to identify prime locations for static source, sideslip ports, and angle-of-attack vanes for the air data system. CFD was used for design of the environmental control system (ECS) inlet and exhaust ports and to plan an unusual wind tunnel evaluation of the inlet. The cabin (pressurization) outflow valves were positioned with CFD. Although still in its infancy with respect to high-lift design, CFD did provide insight to high-lift concepts and was used to assess planform effects. The bulk of the high-lift design work, however, was done in the wind tunnel [5]. Another collaboration between the wind tunnel and CFD involved the use of CFD to determine and refine the corrections applied to the experimental data due to the presence of the wind tunnel walls and model mounting system.
The Next Generation 737-700/600/800/900 (illustrated in Fig. 2), being a derivative of earlier 737s, presented a much more constrained design problem. Again the bulk of the CFD focused on cruise wing design and engine/airframe integration. Although the wing was new, its design was still constrained by the existing wing-body intersection and by the need to maintain manual control of the ailerons in case of a complete hydraulic failure. As with the 777, CFD was used in conjunction with the wind tunnel in the design of the wing-body fairing, modifications to the aft body, and design of the flap track fairings and the high-lift system.
Boeing Commercial Airplanes has leveraged academia- and NASA-developed CFD technology, some developed under contract by Boeing Commercial Airplanes, into engineering tools used in new airplane development. As a result of the use of these CFD tools, the number of wings designed and wind tunnel tested for high-speed cruise lines definition during an airplane development program has steadily decreased (Fig. 3). In recent years, the number of wings designed and tested is more a function of changing requirements during the development program and the need to support more extensive aerodynamic/structural trade studies during development. These advances in developing and using CFD tools for commercial airplane development have saved Boeing tens of millions of dollars over the past 20 years. However, as significant as these savings are, they are only a small fraction of the value CFD delivered to the company.
A much greater value of CFD in the commercial arena is the added value of the product (the airplane) due to the use of CFD. Value to the airline customer is what sells airplanes! Value is added to the airplane product by achieving design solutions that are otherwise unreachable during the fast-paced development of a new airplane. Value is added by shortening the design development process. Time to market is critical in the commercial world, particularly when starting after a competitor has committed a similar product to market. Very important in the commercial world is getting it right the first time. No prototypes are built. From first flight to revenue service is frequently less than one year! Any deficiencies discovered during flight test must be rectified sufficiently for government certification and acceptance by the airline customer based on a schedule set years before. Any delays in meeting this schedule may result in substantial penalties and jeopardize future market success. The added value to the airplane product will produce increased sales and may even open up completely new markets. The result is more profit to both the buyer and seller (who does not have to discount the product as much to make the sale). All this translates into greater market share.
CFD will continue to see an ever-increasing role in the aircraft development process as long as it continues to add value to the product from the customer's point of view. CFD has improved the quality of aerodynamic design, but has not yet had much effect on the rest of the overall airplane development process, as illustrated in Fig. 4. CFD is now becoming more interdisciplinary, helping provide closer ties between aerodynamics, structures, propulsion, and flight controls. This will be the key to more concurrent engineering, in which various disciplines will be able to work more in parallel rather than in the sequential manner as is today's practice. The savings due to reduced development flow time can be enormous!
To be able to use CFD in these multidisciplinary roles, considerable progress in algorithm and hardware technology is still necessary. Flight conditions of interest are frequently characterized by large regions of separated flows. For example, such flows are encountered on transports at low speed with deployed high-lift devices, at their structural design load conditions, or when transports are subjected to in-flight upsets that expose them to speed and/or angle of attack conditions outside the envelope of normal flight conditions. Such flows can only be simulated using the Navier–Stokes equations. Routine use of CFD based on Navier–Stokes formulations will require further improvements in turbulence models, algorithm, and hardware performance. Improvements in geometry and grid generation to handle complexity such as high-lift slats and flaps, deployed spoilers, deflected control surfaces, and so on, will also be necessary. However, improvements in CFD alone will not be enough. The process of aircraft development, itself, will have to change to take advantage of the new CFD capabilities.
The CFD development and application process
In industry, CFD has no value of its own. The only way CFD can deliver value is for it to affect the product. To affect the product, it must become an integral part of the engineering process for the design, manufacture, and support of the product. Otherwise, CFD is just an add-on; it may have some value but its effect is limited. To make CFD an integral part of the Product Development and Support engineering processes, it must get into the hands of the engineers who execute these processes. This is the only way the volume of analysis/design runs necessary to affect the product can be made. Moreover, it is in the Product Development and Support organizations that ownership of the CFD/engineering processes resides, and it is these processes that management relies on when investing billions of dollars in a new airplane development. The CFD developers and ‘‘expert’’ users can certainly contribute, but are only a part of the engineering process.
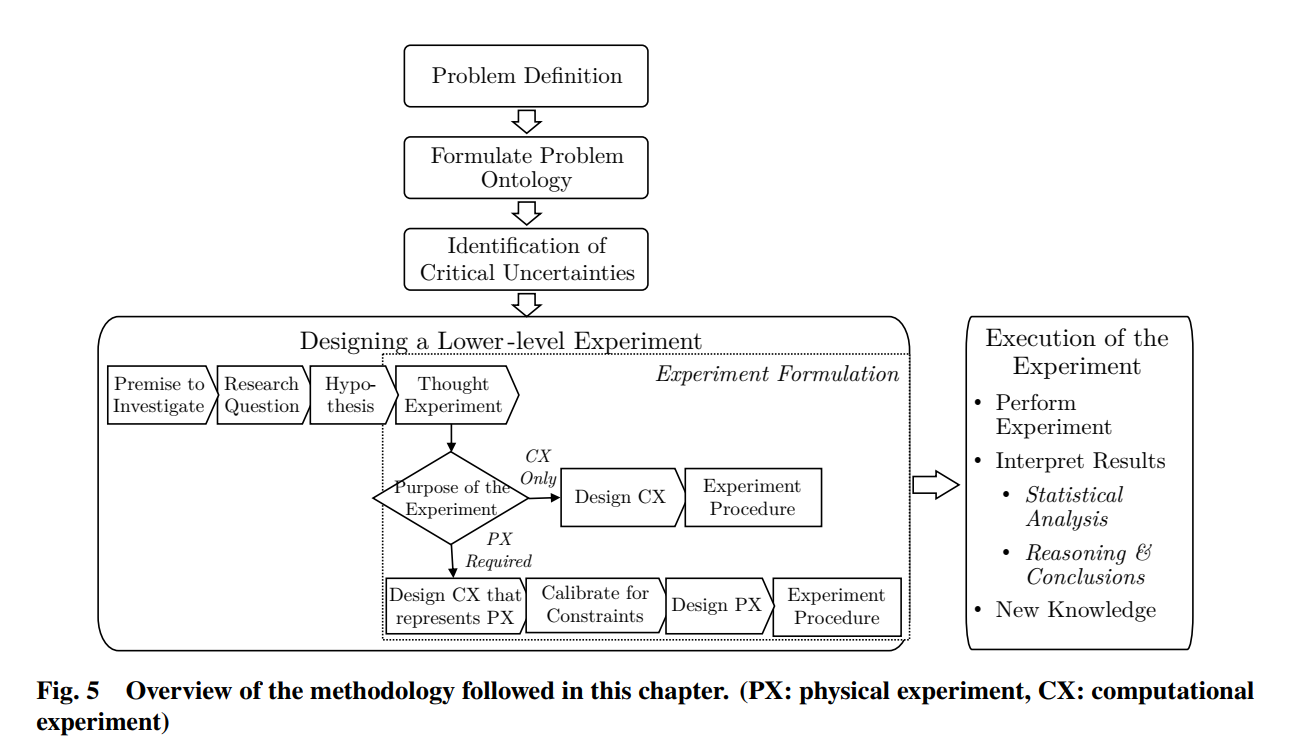
Getting CFD into ‘‘production’’ use is not trivial––it is frequently a multiyear process. There are five distinct phases in the CFD development process. These are illustrated in Fig. 5.
Phase I produces enabling technology algorithms that provide a basic means for solving a given problem. Phase II, which overlaps Phase I, constitutes the initial attempts to explore, validate, and demonstrate a new computational technology. There are some limited pioneering applications at this stage, but the emerging technology is not yet at a state that will produce significant payoff or impact because the technology is still subject to surprise. Hence, managers and design engineers are unwilling at this point to make important, standalone design decisions based on computed results. Such decisions by users do not happen until well into Phase IV.
Many of the code developments end in the middle of Phase II with a contractor report or scientific paper that proclaims, ‘‘Gee whiz, look what can be done.’’ For many codes, this is a good and natural transfer point for industry to assume responsibility for further development, because most of what must occur beyond this point will be unique to the particular needs of each individual industry organization. Of course, this implies that corporate managers must have the wisdom to understand what they must support to turn such a code into a mature and effective capability that will live up to the ‘‘Gee whiz’’ expectations. That requires the time and investment associated with Phases III and IV.
The main outputs of Phase II are demonstrator codes (useful for computational experiments and demonstrations) combined with a vision of what is really needed. Phase III is aimed at supplying the substance of that vision and usually entails a generalization or other modification of Phase II codes (perhaps complete rewrites) combined with a coupling of front- and back-end interfaces to produce user-friendly, well-understood, and maintainable software. Most commercially available (COTS) codes have reached this stage of development. But even at this stage, their contribution or effect on the corporate bottom line is still minimal because engineers and managers don't yet understand how the existence of this new tool will change the engineering process and what it will be used for. They have yet to gain enough confidence to make important, standalone decisions based on the code. That takes time, exposure, and experience.
In the fourth phase, the payoff or affect of a code grows rapidly. Phase IV entails ‘‘applications research,’’ where design engineers, management, and code developers work together to learn how this new capability will enter into and change the aerodynamic design process. The applications research endeavor requires people with broad backgrounds who can ask the right questions of the algorithm researchers, and code developers who can intelligently question experimental data when test-theory comparisons don't agree. Both must also be good physicists, for it is not unusual to find that the short-comings lie neither in the experiment nor in the quality of the computations, but in the fact that the theoretical model assumed in the computations was not an adequate description of the real physics. Need for code refinements that were not anticipated invariably surface during this phase and these refinements often require more algorithm research, additional geometry preprocessors, and so on. Over time, the requests for additions or refinements diminish until the code settles down to occupy its proper niche in the toolbox, and design engineers and managers have learned the capabilities, limitations, and proper applications of this now-mature code. Without the investments in Phase IV, the enormous pay-off of having a mature capability in Phase V will not happen. An attempt to bypass Phase IV by taking a code developed by algorithm researchers and placing it directly in the hands of design engineers, who may not understand the underlying theoretical models, algorithms, and possible numerical idiosyncrasies, usually results in a prolonged period of frustration and unreliability that leads to abandonment of the code.
Product Development engineers must be able to focus on engineering processes and have little time for manipulating the CFD ‘‘process’’ (i.e., codes must be very user oriented). Stable, packaged software solutions enable and promote consistent processes. These not only put CFD into the hands of the Product Development/Product Support engineers but also allow the ‘‘expert’’ user to get fast results with reduced variation. Integrated packaged software solutions combine various components to go from ‘‘lofts to plots’’ in the time scale consistent with a fast-paced engineering program. These packages include scripted packages for ‘‘standard’’ configurations, geometry and grid/paneling generation components, flow solvers, and postprocessing components for analyzing the results. These are all placed under some form of software version control to maintain consistency.
A key component of CFD and most engineering processes is geometry. CAD systems, such as CATIA, dominate most geometry engineering needs. However, these systems are designed for component design and definition and are not well suited to CFD use. A key component of many Boeing Commercial Airplanes CFD processes is AGPS––Aero Grid and Paneling System [6]. AGPS is a geometry software tool implemented as a programming language with an interactive graphical user interface. It can be dynamically configured to create a tailored geometry environment for specific tasks. AGPS is used to create, manipulate, interrogate, or visualize geometry of any type. Since its first release in 1983, AGPS has been applied with great success within The Boeing Company to a wide variety of engineering analysis tasks, such as CFD and structural analysis, in addition to other geometry-related tasks.
Computing resources consisting of high-end computing and graphics workstations must also be integrated. Seamless mass data storage must be available to store the vast amount of information that will be generated during the engineering application. These resources require dedicated computing system administration. The software control and computing system administration are necessary to free the engineers to focus their work on the engineering processes and not be consumed by the ‘‘computing’’ process.
Close customer involvement and acceptance is absolutely essential to deriving value from CFD. Customers are responsible for implementing the engineering process that will use CFD. They own the process, they determine what CFD, if any, they will depend on to carry out their assigned tasks. They are being graded on the engineering tasks they accomplish not on which CFD codes they use. Their use and trust of CFD is based on a long-term relationship between supplier and user. This relationship has engaged the customer early on in demonstrations of a new code or new application of an existing code. Validation is an on-going process, first of cases of interest to the customer, and then of the customer's ability to implement the new tool. Frequently, parallel applications are undertaken in which the customer continues with the existing tools while the supplier/developer duplicates the process with the new tool. This is especially the case when the new tool may enable the development of an entirely new process for executing the engineering task.
The long-term relationship with the customer is essential from another point of view. Until recently, project engineers, without exception, initially rejected every new CFD development that later became the primary CFD analysis and design tool in Boeing Commercial Airplanes Product Development and Product Support organizations. Every new or proposed CFD capability was initially viewed as too difficult to use, too costly to run, not able to produce timely results, not needed, and so on. ‘‘Just fix what we already have,’’ the customer would tell the developers. The customers had a point. Not until the new CFD technology had been integrated with the customer's preprocessing/postprocessing tools and computing system, validated to the customer's program, guaranteed of long-term support, and committed to continuous development and enhancement would the new technology be useful to them.
This made it difficult for the developers to propose new Phase I, II and III efforts. In particular, the initiation and continual defense of Phase I efforts demanded clear and unwavering vision. True vision invariably requires a fundamental understanding of both needs and means. As customers generally did not have the specialized algorithmic knowledge underlying CFD numerics, it was incumbent on the developers to acquire a thorough understanding of customer needs and concerns. The developers learned they could not just throw a new CFD tool over the fence and expect the customer to use it no matter how good it might be. The customer was interested in getting an engineering job done and not in the CFD tool itself! The process of thoroughly understanding customer issues took many years, and early Phase I, II, and III efforts were mostly ‘‘technology push’’ efforts, which had to be funded by NASA or other Government agencies. As these efforts progressed to Phase IV and V, and the developers established a track record for producing useful capabilities, the situation gradually changed.
Each success allowed the developers a little more leeway. Often they spotted ‘‘niche’’ needs that could be satisfied by the introduction of their new technology. It was felt that when the users were satisfied with the usability and utility of the technology in these areas they would then be willing to consider whether or not replacing their old tools in other areas might offer distinct advantages. Once the users accepted a new capability, they often became very innovative and applied the codes in unanticipated ways, perpetually keeping the developers and validation experts in an anxious state. Most of the new applications were, in fact, legitimate, and the developers had to run fast to understand the implications involved as well as to try and anticipate future application directions. As time went on, code developers, application experts, and project engineers began understanding each other's functions and issues, and a certain amount of trust developed. Gradually, CFD became a ‘‘pull’’ rather than ‘‘push’’ technology. This transformation was greatly facilitated by the rotation of top engineers between these functions.
Today in Boeing Commercial Airplanes, more than 20,000 CFD runs a year are made to support product development and the various existing product lines. More than 90% of these runs are done by production engineers outside the research group. The CFD methods in use provide timely results in hours or days, not weeks or months. Sufficient experience with the methods has given management confidence in their results. This means that solutions are believable without further comparison of known results with experiment, that the CFD methods contain enough of the right physics and resolve the important physical and geometric length scales, that the numerics of the method are accurate and reliable, and that the CFD tools are already in place––for there is no time to develop and validate new methods. Most of all, management is convinced that the use of CFD makes economic sense. A look at the history of CFD at Boeing Commercial Airplanes will show how we got to this level of use.
Chronology of CFD capability and use
CFD today covers a wide range of capabilities in terms of flow physics and geometric complexity. The most general mathematical description of the flow physics relevant to a commercial transport is provided by the Navier–Stokes equations. These equations state the laws of conservation of mass, momentum, and energy of a fluid in thermodynamic equilibrium. Unfortunately, direct solutions to these equations for practical aircraft configurations at typical flight conditions are well beyond the capabilities of today's computers. Such flows include chaotic, turbulent motions over a very wide range of length scales. Computations for the simulations of all scales of turbulence would require solving for on the order of 10¹⁸ degrees of freedom!
Fortunately, solutions to simplified (and more tractable) forms of these equations are still of great engineering value. Turbulent flows may be simulated by the Reynolds equations, in which statistical averages are used to describe details of the turbulence. Closure requires the development of turbulence models, which tend to be adequate for the particular and rather restrictive classes of flow for which empirical correlations are available, but which may not be currently capable of reliably predicting behavior of the more complex flows that are generally of interest to the aerodynamicist. Use of turbulence models leads to various forms of what are called the Reynolds-averaged Navier–Stokes equations.
For many aerodynamic design applications, the flow equations are further simplified to make them more amenable to solution. Neglecting viscosity leads to the Euler equations for the conservation of mass, momentum, and energy of an inviscid fluid. Fortunately, under many flight conditions the effects of viscosity are small and can be ignored or simulated by the addition of the boundary layer equations, a much simplified form of the Reynolds-averaged Navier–Stokes equations.
The introduction of a velocity potential reduces the need to solve five nonlinear partial differential equations (that make up the Euler equations) to the solution of a single nonlinear partial
differential equation known as the full potential equation. However, the potential approximation assumes an inviscid, irrotational, isentropic (constant entropy) flow. Potential solutions can adequately simulate shock waves as long as they are weak, which is the normal case for commercial transport configurations.
Further simplifications eliminate all the nonlinear terms in the potential equation, resulting in the Prandtl–Glauert equation for linear compressible flows, or the Laplace equation for incompressible flows. The use of these equations is formally justified when the vehicle is relatively slender or thin and produces only small disturbances from freestream flow.
In the following sections, we describe the CFD capability most heavily used at Boeing Commercial Airplanes in Seattle over the last 30 years. For the purposes of a rough chronological summary, we can say the following. Before 1973, the main codes employed by project engineers involved linearized supersonic flows with linearized representations of the geometry or else 2D incompressible flows. From 1973 to 1983, panel methods, which could model complex geometries in the presence of linear subsonic and supersonic flows, took center stage. The nonlinear potential flow/coupled boundary layer codes achieved their prime from 1983 to 1993. Their Euler counterparts came into use later in that timeframe. From 1993 to 2003, Reynolds averaged Navier–Stokes codes began to be used with increasing frequency. Clearly, much of the development and demonstration work leading to the widespread use of these codes occurred from five to 10 years earlier than these dates. It is important to note that a considerable length of time is often required for a code to achieve the Phase V level of maturity. It is also important to realize that once a code achieves this level of maturity and is in use and accepted by the user community, it tends to remain in use, even though improved capability at the Phase III or IV level may be available.
The Boeing panel code, A502, remains in some use today, even though its underlying technology was developed almost 30 years ago. The full potential code TRANAIR still receives widespread and heavy use.
4.1. Linear potential flow
4.1.1. First generation methods––early codes
The flow physics described by the early linear methods were greatly simplified compared to the ‘‘real’’ flow. Similarly, the geometric fidelity of the actual configuration also had to be greatly simplified for the computational analysis to fit within the speed and size constraints of the computers of that era. In spite of such seemingly hopeless limitations, these early CFD methods were successfully applied during the supersonic transport development programs of the late 1960s––the Anglo-French Concord and the United States/Boeing SST. The need for computational help in the aerodynamic development of these aircraft stemmed from two factors. First, there was the relative lack of experience in designing supersonic cruise aircraft (the first supersonic flight had occurred only 15 years earlier). Second, there is great sensitivity of supersonic wave drag to details of the aircraft design. Thus, the challenge of developing a viable low-drag design through empirical ‘‘cut and try’’ demanded whatever computational help was available. The opportunity to use simplified computational methods resulted because the design requirements for low supersonic wave drag led to thin, slender vehicles that minimized ‘‘perturbing’’ the airflow. These characteristics were consistent with the limitations of the linearized supersonic theory embedded in the early CFD codes. These codes included TA80 [7], a Supersonic Area Rule Code based on slender body theory; TA139/201 [8], a Mach Box Code based on linearized supersonic theory; and TA176/217 [9], a Wing-Body Code based on linear potential flow theory with linearized geometry representations. These codes ran on IBM7094 machines. The good agreement with test data predicted by these linear theory methods for a drag polar of the Boeing SST model 733-290 is shown in Fig. 6. This was a linear theory optimized design of the configuration that allowed Boeing to win the SST design development Government contract. The resulting supersonic transport designs ended up looking as they did, in part, because the early CFD codes could not handle more geometrically complex configurations.
The linear aerodynamics of the Wing-Body Code was later combined with linear structural and dynamic analysis methods in the FLEXSTAB [10] system for the evaluation of static and dynamic stability, trim state, inertial and aerodynamic loading, and elastic deformations of aircraft configurations at supersonic and subsonic speeds. This system was composed of a group of 14 individual computer programs that could be linked by tape or disk data transfer. The system was designed to operate on CDC-6000 and -7000 series computers and on the IBM 360/370 computers. A very successful early application of FLEXSTAB was the aeroelastic analysis of the Lockheed YF-12A as part of the NASA Flight Loads program. Thirty-two flight test conditions ranging from Mach 0.80 to 3.0 and involving hot or cold structures and different fuel loading conditions were analyzed at several load factors [11].
4.1.2. First generation methods––TA230
By 1973, 3D subsonic panel methods were beginning to affect the design and analysis of aircraft configurations at Boeing. Subsonic panel methods had their origins with the introduction of the Douglas Neumann program in 1962 [12]. This program was spectacularly successful for its time in solving the 3D incompressible linear potential flow (Laplace) equation about complex configurations using solid wall (Neumann) boundary conditions. The numerical method represented the boundary by constant strength source panels with the strengths determined by an influence coefficient equation set relating the velocities induced by the source panels to the boundary conditions. The lack of provision for doublet panels limited the class of solutions to those without potential jumps and hence without lift. One of the first computer programs for attacking arbitrary potential flow problems with Neumann boundary conditions [13,14] combined the source panel scheme of the Douglas Neumann program with variations of the vortex lattice technique [15]. This program became known as the Boeing TA230 program. A very useful feature of this program was the ability to handle, in a logical fashion, any well-posed Neumann boundary value problem. From its inception, the method employed a building block approach wherein the influence coefficient equation set for a complex problem was constructed by simply assembling networks appropriate to the boundary value problem. A network was viewed as a paneled surface segment on which a source or doublet distribution was defined, accompanied by a properly posed set of Neumann boundary conditions. The surface segment could be oriented arbitrarily in space and the boundary conditions could be exact or linearized. Several doublet network types with differing singularity degrees of freedom were available to simulate a variety of physical phenomena producing discontinuities in potential. Compressibility effects were handled through scaling. These features combined to allow the analysis of configurations having thin or thick wings, bodies, nacelles, empennage, flaps, wakes, efflux tubes, barriers, free surfaces, interior ducts, fans, and so on.
By 1973, Boeing had acquired a CDC 6600 for scientific computing, which allowed the TA230 program to solve problems involving hundreds of panels. This was sufficient to model full configurations with the fidelity necessary to understand component interactions.
One of the most impressive early uses of the TA230 code was in the initial design phase of the B747 Space Shuttle Carrier Aircraft (SCA). The purpose of the initial design phase was to define the modifications needed to accomplish the following missions: to ferry the Space Shuttle Orbiter; to air-launch the Orbiter; and to ferry the external fuel tank. To keep the cost of the program to a minimum, CFD was extensively used to investigate the Orbiter attitude during the ferry mission, the Orbiter trajectory and attitude during the launch test, and the external tank location and attitude during the ferry mission. At the conclusion of the design phase, the final configurations selected were tested in the wind tunnel to verify predictions. A typical example of a paneling scheme of the B747 with the Space Shuttle Orbiter is depicted in Fig. 7. In this example, the Orbiter incidence angle was 8 deg with respect to the B747 reference plane. The predicted lift coefficient, CL, as a function of wing angle of attack for this configuration is shown in Fig. 8. The agreement between the analyses and wind tunnel data shown in this figure is excellent.
TA230 was used with TA378 [16], a 3D Vortex Lattice Method with design/optimization capability, to develop winglets for a KC-135 aircraft. Wind tunnel tests confirmed a 7–8% drag reduction in airplane drag due to the installation of these winglets [17].
Another early CFD success was the improvement of the understanding of the interference drag of a pylon-mounted engine nacelle under the wing. The existence of unwanted interference drag had been revealed by wind tunnel testing, but the physical mechanism of the interference was still unknown. To avoid the interference drag, it is common practice to move the engine away from the wing. The resulting additional weight and drag due to the longer engine strut must be balanced against the potential interference drag if the engine is moved closer to the wing. CFD studies with TA230 along with specialized wind tunnel testing in the mid-1970s, provided the necessary insight into the flow mechanism responsible for the interference. This understanding led to the development of design guidelines that allowed closer coupling of the nacelle to the wing [18]. The Boeing 757, 767, 777, 737-300/400/500 series, Next Generation 737/600/700/800/900 series, and the KC-135R are all examples of aircraft where very closely coupled nacelle installations were achieved without incurring a significant drag penalty.
4.1.3. Second generation linear potential flow method––PANAIR/A502
The success of the TA 230 code in modeling complete vehicle configurations and component interactions created a strong demand among Boeing aerodynamicists for CFD analyses and was undoubtedly the key factor that initiated the paradigm shift toward acceptance of CFD as an equal partner to the wind tunnel and flight test in the analysis and design of commercial aircraft. However, the paradigm shift was slowed by the fact that the code had to be run by experts possessing specialized knowledge, some of which was totally unrelated to aerodynamics. In fact, it often took weeks requiring the expertise of an engineer having months or years of experience with the method to set up and run a complex configuration. To some extent this was unavoidable; to correctly model a complex flow for which no previous user experience was available, the engineer had to understand the mathematical properties and limitations of potential flow. Nevertheless, once the boundary value problem was formulated, the user still had to contend with certain numerical idiosyncrasies and inefficiencies that required adherence to stringent paneling rules, frequently incompatible with the complex geometrical contours and rapidly changing aerodynamic
length scales of the vehicle under analysis. Such difficulties were directly related to the use of flat panels with constant source and doublet strengths. Methods employing these features were quite sensitive to panel layout. Numerical problems arose when panel shapes and sizes varied, and fine paneling in regions of rapid flow variations often forced fine paneling elsewhere. In addition, excessive numbers of panels were often required since numerical accuracy was strongly affected by local curvature and singularity strength gradient. These problems placed severe limitations on the development of automatic panelers and other complementary aids aimed at relieving the user of the large amount of handwork and judgments associated with producing accurate numerical solutions.
Consequently, a method was developed under contract to NASA to enhance practical usability by improving upon the flat, constant singularity strength panels employed in the construction of networks [19]. This method featured the use of curved panels and higher order distributions of singularities. Source and doublet strengths were defined by least square fits of linear and quadratic splines to discrete values located at specific points on the networks. Higher order influence coefficients were obtained using recursion relations with the standard low order coefficients as initial conditions. Boundary conditions were enforced at the same or other discrete locations depending on their type. Virtually any boundary condition that made sense mathematically was provided for. In particular, the incorporation of Dirichlet boundary conditions not only offered the opportunity to design surface segments to achieve desired pressure distributions, but also clarified the nature of the boundary value problem associated with modeling viscous wakes and propulsion effects. Robin boundary conditions provided for the modeling of slotted walls, which allowed for direct comparisons of CFD results with wind tunnel data. These features were incorporated in the NASA code known as PANAIR and the Boeing code known as A502. The latter code was generalized to treat supersonic flows [20], free vortex flows [21], and time harmonic flows [22]. In the supersonic case, upwinding was achieved by forward weighting the least square singularity spline fits.
The numerics incorporated into A502 solved a number of usability issues. Fig. 9 clearly demonstrates the relative insensitivity and stability of computed results to paneling. This insensitivity encouraged project users to apply the code and trust results. In addition, the boundary condition flexibility allowed users to experiment with various types of modeling, leading to a wide variety of applications never entirely envisioned by the developers.
The versatility of A502 paid off when a ‘‘surprise’’ was encountered during the precertification flight testing of the then new 737-300. The aircraft was not demonstrating the preflight wind tunnel based prediction of take-off lift/drag ratio. A fix was needed quickly to meet certification and delivery schedules. Specialized flight testing was undertaken to find the cause and to fix the performance shortfall. A CFD study was immediately undertaken to enhance understanding and provide guidance to the flight program. Eighteen complete configuration analyses were carried out over a period of three months. These included different flap settings, wind tunnel and flight wing twist, flow through and powered nacelle simulations, free air and wind tunnel walls, ground effect, seal and slotted flaps, and other geometric variations [23]. These solutions explained and clarified the limitations of previous low-speed wind tunnel test techniques and provided guidance in recovering the performance shortfall through ‘‘tuning’’ of the flap settings during the flight testing. The aircraft was certified and delivered on schedule. A comparison of the computation L/D predictions with flight is shown in Fig. 10.
A502 studies have been used to support other flight programs on a time-critical basis. In particular, the code was used to support engine/airframe installation studies in the early 1980s [24], to evaluate wind tunnel tare and interference effects, and to provide Mach blockage corrections for testing large models. In addition, the code was used for the design of the wingtip pod for the Navy E6-A, a version of the Boeing 707. No wind tunnel testing was done before flight. The FAA has accepted A502 analysis for certification of certain aircraft features that were shown to have minimal change from previous accepted standards. Finally, A502 was used to develop a skin waviness criteria and measurement technique that led to the virtual elimination of failed altimeter split testing during the first flight of every B747-400 aircraft coming off the production line. Initially, one of every three aircraft was failing this test, requiring several days down time to fix the problem. The A502-based procedure could identify excessive skin waviness before first flight and led to manufacturing improvements to eliminate the root cause of the problem.
A502 is still used today to provide quick estimates for preliminary design studies. A relatively new feature of the code takes advantage of available linear sensitivities to predict a large number of perturbations to stability and control characteristics and stability derivatives, including control surface sensitivities. Virtual control surface deflections and rotary dynamic derivatives are modeled through surface panel transpiration. Stability derivatives, such as the lift curve slope or directional stability, are calculated automatically. A typical application may involve 20 subcases submitted in a single run, with solutions available in an hour or so. Within the limitations of the code, all major stability and control derivatives can be generated in a single run (at a single Mach). The method is typically used to calculate increments between similar configurations. The code was recently used to calculate stability and control increments between a known baseline and a new configuration. A total of 2400 characteristics were computed for eight configurations by one engineer in a two-day period!
4.2. Full potential/coupled boundary layer methods
4.2.1. A488/A411
Since Murman and Cole [25] introduced a numerical solution method for the transonic small disturbance equation in the early 1970s, computational fluid dynamics method development for nonlinear flows has progressed rapidly. Jameson and Caughey [26] formulated a fully conservative, rotated finite volume scheme to solve the full potential equation––the well-known FLO27/28 codes. The Boeing Company acquired the codes and invested a significant amount of effort to advance the capability from Phase II to Phase V. Convergence reliability and solution accuracy were enhanced. To allow transonic analyses over complex transport configurations, a numerical grid generation method based on Thompson's elliptic grid generation approach [27] was developed [28] and tested extensively for wing or nacelle alone, wing-body, and wing-body-strut-nacelle configurations. The potential flow solvers FLO27/28 coupled with the 3D finite difference boundary layer code A411 [29] and the 3D grid generation code formed the major elements of the Boeing transonic flow analysis system, A488––the most heavily used analysis code at Boeing from late 1970s to early 1990s. The production version of the A488 system, illustrated in Fig. 11, included a number of preprocessing and postprocessing programs that could handle the complete analysis process automatically for specific configuration topologies––a truly useable code for design engineers. This integrated packaged combined the various software components to go from ‘‘lofts to plots’’ in the time scale consistent with a fast paced engineering program––overnight!
Fig. 12 shows a comparison of A488 results obtained by project engineers with wing pressure distributions measured in flight on a 737-300. The computational model consisted of the wing, body, strut, and nacelle. The wing definition included the estimated aeroelastic twist for the condition flown. Although the character of the pressure distribution on the wing changes dramatically across the span, the computational results agree reasonably well with the measured data.
The Boeing Propulsion organization also employed a full potential/coupled boundary layer code called P582. It was developed at Boeing and used a rectangular grid [30] and multigrid acceleration scheme [31]. P582 was used extensively for engine inlet simulation and design in the late 1970s and 1980s and is still used in the Propulsion organization for various nacelle inlet simulations.
4.2.2. TRANAIR
By 1983, complex configurations were routinely being analyzed by project engineers using panel methods. Surface geometry generation tools were maturing, and users took for granted the ability to add, move, or delete components at will; readily change boundary condition types; and obtain numerically accurate solutions at reasonable cost in a day or two. On the other hand, the nonlinear potential flow codes required expert users and considerable flow time to obtain converged and accurate results on new and nonstandard configurations. Often, geometrical simplifications had to be made jeopardizing the validity of conclusions regarding component interactions. Clearly, the nonlinear nature of the flow was responsible for numerous difficulties. The development of shocks in the flowfield prolonged convergence, especially if the shocks were strong and prematurely set in the wrong location. Moreover, weak and double shocks were often not captured accurately, if at all. Boundary layer coupling contributed problems as well, especially as separation was approached. Often, the boundary layer displacement effect had to be fixed after a certain number of iterations, leading to questionable results. Experts became very good at circumventing many of these problems; however, the one problem that could not readily be overcome was the necessity to generate a volume grid to capture nonlinear effects.
Even today, volume grid generation is one of the main barriers to routine use of nonlinear codes. Often the creation of a suitable grid about a new complex configuration can take weeks, if not months. In the early 1980s, the situation was far worse, and suitable grids were readily available only for standard and relatively simple configurations. Because of the enormous promise demonstrated by existing nonlinear methods, the panel method developers at Boeing were awarded a contract from NASA to investigate alternatives to surface fitted grid generation. In the next few paragraphs, we describe some of the technical issues that arose during this contract. They are of interest to this paper in that they followed directly from a ‘‘needs and usability’’ starting point rather than the usual ‘‘technology discovery’’ starting point. To a large extent, this has characterized the CFD development efforts at Boeing.
The developers started with a rather naıve approach, i.e., take an A502 paneling, with which the project users were already familiar, and embed it in a uniform rectangular grid to capture nonlinear effects (Fig. 13). This approach logically led to a sequence of subproblems that had to be addressed in turn [32]. First, one could hardly afford to extend a uniform grid into the far field to ensure proper far field influence. However, if the flow was assumed to be linear outside a compact region enclosing the configuration, one could use linear methods to obtain the far field influence. A discrete Green's function for the Prandtl–Glauert equation was constructed, which incorporated the effect of downstream sources and sinks resulting from wakes. This Green's function was applied using FFTs and the doubling algorithm of Hockney [33], a standard technique in astrophysics. The net effect was the same as if the uniform grid extended all the way to infinity, the only approximation being the assumption of linearity outside a compact box. As a byproduct of this solution, the user no longer had to estimate a suitable far field stretching ratio.
The next problem that had to be addressed was how to handle the intersections of the grid with the paneling and how to apply boundary conditions. The developers decided to use a finite element approach based on the Bateman variational principle [34]. Upwinding was achieved by factoring the density at the centroid of the elements out of the stiffness integrals and then biasing it in an upwind direction. The elements intersecting the paneled boundary were assumed to have linear basis functions regardless of their shapes. Stiffness matrix integrals were then evaluated over the subset of the elements exposed to the flowfield. The integration was performed recursively using volume and then surface integration by parts. Additional surface integrals were added to impose the same variety of boundary conditions as available in A502.
The main problem with a uniform rectangular grid is its inability to capture local length scales of the geometry and flow. Consequently, grid refinement was an absolutely necessary feature of the approach. However, it was felt that solution adaptive grid refinement was necessary in any event to ensure accuracy, especially if the code was to be used by project engineers without the aid of the developers. The refinement mechanism was relatively straightforward, just divide each rectangular grid box into eight similar boxes (Fig. 14) and keep track of the refinement hierarchy using an efficient oct-tree data structure.
Development of a suitable error indicator was another matter, however. Mathematical theory certainly offered guidance here, but a surprising amount of engineering knowledge had to be injected into the process. A typical ‘‘gotch-ya’’ with a pure mathematical approach was the tendency of the refinement algorithm to capture the precise details of a wing tip vortex all the way from the trailing edge to the end of a wind tunnel diffuser.
The existence of refined grid complicated the design of a solution algorithm. Multigrid methods were somewhat of a natural here, but the developers were partial to direct solvers, as they had turned out to be so flexible for the panel codes, especially when it came to implementing unusual boundary conditions and coupling boundary layer equations and unknowns. They adopted a damped Newton method approach, with the Jacobian solved using a preconditioned GMRES iterative algorithm. A sparse direct solver was used as a preconditioner. Even with nested dissection ordering, the cost and storage for a complete factorization was prohibitive, hence they settled on the use of an incomplete factorization employing a dynamic drop tolerance approach, whereby small fill-in elements were dropped as they were formed. The method was surprisingly efficient and robust. As a rule, decomposition of the Jacobian resulted in fill-in factors of less than two and constituted less than 10% of the total run cost, even for grids having more than a million nodes.
Early versions of TRANAIR used the A411 boundary layer code in an indirectly coupled mode in much the same manner as A488. However, the desired convergence reliability was never achieved, and the shock boundary layer interaction model was occasionally suspect. About this time, Drela [35] developed an exceedingly accurate 2D integral boundary layer that he directly coupled with his 2D Euler solver. With Drela's help, the TRANAIR development team modified this boundary layer to incorporate sweep and taper effects and integrated it into the code. In this connection, the use of a direct solver was invaluable. The resultant code turned out to be very accurate for transport configurations and agreement with experiment was considered by project users to be quite remarkable.
As TRANAIR received increasing use, a number of enhancements were added. To model powered effects, regions of non-freestream but constant total temperature and pressure were simulated along with appropriate shear layer effects [36]. Far field drag calculations were added, which later led to the ability to perform aerodynamic optimization. Time harmonic capability was created for stability and control calculations. Aeroelastic effects were simulated by adding structural unknowns and equations to the system [37]. Here again the use of a sparse solver was invaluable.
Without question, the development of the TRANAIR code strongly benefited from the work and experiences of CFD pioneers such as Murman [25], Jameson [26], Hafez [38], Cebeci [39], McLean [29], Drela [35], and others. Nevertheless, about 10 major and 30 minor algorithms had to be developed or adapted. A few were quite far from the mainstream CFD efforts of the time and required considerable effort. It took almost five years of research and development before a truly useful result could be produced (1989). The TRANAIR code ultimately evolved into the Boeing workhorse aerodynamic code of the 1990s and up to the current time for analyzing flows about complex configurations. TRANAIR was heavily used in the design of the 777, the 737NG, and all subsequent modifications and derivatives to the Boeing Commercial Airplanes fleet. Since 1989, it has been run to completion more than 70,000 times on an enormously wide variety of configurations, some of which were not even vehicles. It has had about 90 users in Boeing. An older version of the code was used by NASA, the Air Force, the Navy, and General Aviation. In 2002, TRANAIR was run to completion at Boeing more than 15,000 times, which is considerable use for a complex geometry CFD code. If we had to choose one single technical feature of TRANAIR that was responsible for such widespread use, we would choose solution adaptive grid refinement. In retrospect, while this feature was intended to improve accuracy, its main benefit was to greatly relieve the user of the burdensome and labor-intensive task of generating a volume grid.
Even with substantially simplified gridding requirements, inputting a general geometry CFD code and processing the outputs are still formidable tasks. An essential enabler for TRANAIR has been the development of a packaged process for inputting ‘‘standard’’ configurations. By ‘‘standard,’’ we mean those configuration types that have been scripted in the various components that make up the process. Configurations not included in the ‘‘standard’’ can still be analyzed but will not benefit from the same degree of automation. This package, illustrated in Fig. 15, is compatible and takes advantage of common Boeing Commercial Airplanes processes for geometry and postprocessing. At the center of this process is the TRANAIR flow solver. AGPS scripts have been developed to automate the paneling of ‘‘standard’’ configurations from AGPS lofts. AGPS scripts have also been developed to generate the input deck for the TRANAIR solver. These inputs define the flight conditions, solution adaptive gridding strategy, and the boundary layer inputs for ‘‘standard’’ configurations. A UNIX script is available to generate the various job control files to execute the solver on several types of computers. The TRANAIR solver generates several files for restarts of the solver and output processor, output files for various aerodynamic parameters, and a file for flowfield parameters. A special-purpose code, compatible with the unique TRANAIR grid structure, is available to view the flowfield properties. The package enables setting up and submitting for solution a ‘‘standard’’ configuration from AGPS lofts in one or two hours. Complete solutions from ‘‘lofts to plots’’ are frequently available in less than 12 h. ‘‘Standard’’ configurations include transport configurations including, for example, four-engine 747-like aircraft with underwing struts and nacelles and vertical and horizontal stabilizer with boundary layer on both wing and body.
During the aerodynamic design of the Boeing 777 in the early 1990s, the risk of significant interference drag due to the exhaust from the large engines was revealed through TRANAIR analysis. Neither the earlier linear-based CFD methods nor conventional wind tunnel testing techniques, which did not simulate the exhaust, would have detected this potential problem. Only a very expensive powered-nacelle testing technique could assess these interference effects. Three different manufacturer's engines were being considered for the new aircraft. Using the powered testing technique to develop the engine installations would have added considerable expense. Moreover, such a wind tunnel based development would have unacceptable design flow time. Nonlinear transonic TRANAIR analysis by the product development engineers made it practical to address these installation problems including the effects of the engine exhaust flows in a timely manner. Had these problems gone undetected until late in the aircraft's development when the powered testing is usually done, any fixes would have been extremely expensive to implement.
Fig. 16 shows a comparison of TRANAIR results with test data from a similar configuration. TRANAIR's ability to provide insight to design changes allowed a close ‘‘Working Together’’ relationship between the various Boeing engineering disciplines and the engine manufacturers. It is noteworthy that the exhaust system of all three engines models is very similar in design, a feature found only on the 777. Key to the success of this application was the ability to model enough of the relevant physics and to provide solutions quickly enough to support the development schedule. The effect of CFD on the project was to provide information facilitating a closer working relationship between design groups. This enabled detecting problems early in the development process, when fixing or avoiding them was least expensive.
TRANAIR continues to see extensive use as the primary tool for transonic aerodynamic evaluation and design of commercial aircraft configurations. It is well suited for analysis in the attached and mildly separated flow portion of the flight envelope. For conditions with strong viscous interactions, one must resort to using the Navier–Stokes equations.
4.2.3. BLWF
The BLWF code was developed by researchers at the Central Aerohydrodynamic Institute (TsAGI) and enhanced under contract with the Boeing Technology Research Center in Moscow, CIS [40]. It saw it first use at Boeing in 1994. The BLWF technology was very similar to the technology of the A488 system that had been developed internally at Boeing. However, it differed from A488 in that it had been designed and tuned for workstations and later, PC computing systems, instead of the large vector supercomputers that had been the main computational modeling tool within Boeing Commercial Airplanes. The tool was very responsive, providing solutions within minutes, rather than hours. The rapidity of response, along with the significant cost-of-use reduction by hosting on less expensive hardware systems, changed the nature of use of the modeling tool. New applications, such as Reynolds number corrections for wing loads, have become feasible with such a tool. This application requires solutions for about a dozen Mach numbers over a range of angles of attack (five to 10). Use of BLWF allows a database of hundreds of solutions to be generated in a matter of a few hours, rather than days or weeks. The code has also been used extensively in the preliminary design stage of aircraft definition. At this point in the airplane development cycle, there are typically a large number of significant changes in the aircraft definition, along with a need to understand the behavior of the configuration over a large range of conditions. BLWF allows more realistic modeling of the flight characteristics than other Preliminary Design methods and also provides an ability to obtain the information rapidly, allowing more effective cycling of the preliminary design through the evolution of an aircraft.
4.3. Euler/coupled boundary layer methods
The use of full potential/boundary layer coupling code reaches its limit in predicting airplane performance at off-design conditions where significant shock induced flow separations or vortex flows generated from sharp edges of the configuration, occur in the flowfield. The boundary layer approximation breaks down, and the irrotational/isentropic flow assumption is not a good approximation for such flow conditions. Moreover, wake locations must be estimated a priori, preventing the accurate analysis of flows where vortex interactions are an important feature.
Algorithm research in the early 1980s focused on solution of the Euler equations––the governing equations for inviscid fluid flows. The Boeing version of an Euler/boundary layer coupling code––A588 is based on FLO57 [41] coupled with the same boundary layer code A411 used in A488. The code also introduced a capability for simulating engine inlet and exhaust flows with various total pressures and total temperatures, as well as propfan engine power effects through the use of an actuator disk concept. A588 was the main analysis tool for isolated nacelle development studies until very recently. It provided accurate predictions of nacelle fan cowl pressure distributions, as well as fan cowl drag rise. The multiblock 3D Euler code was used extensively for the simulation of the propfan engine on The Boeing 7J7 program during the mid-1980s, as shown in Fig. 17. A key application was the evaluation of propfan engine installation effects on tail stability characteristics––including simulations that could not be accomplished in the wind tunnel.
Another Euler/integral boundary layer coupling code––A585, based on Drela and Giles [42], was developed in mid-1980s for 2D airfoil analysis and design. This code has been used extensively for advanced airfoil technology development, an essential capability for airplane product development engineers.
4.4. Navier–Stokes methods
The limitation of full potential or Euler/boundary layer coupling codes to flow regimes without significant flow separation leads to the development and application of solutions to Navier–Stokes equations, which are valid over the whole range of flight regime for most commercial airplanes. Finite difference schemes [43] or finite volume schemes with either artificial numerical dissipation [44] or Roe's upwind scheme [45] were developed and tested extensively during the late 1980s and early 1990s. At the same time, development of turbulence models for attached and separated flow simulations progressed rapidly. The simple zero equation Baldwin/Lomax model [46] was used extensively during the early stage of Navier–Stokes code applications. Later on, the Baldwin/Barth one equation model [47], the Spalart/Allmaras one equation model [48], together with Menter's shear-stress transport k–w model [49], were available, and were used for a wide range of flight conditions including massively separated flows.
4.4.1. Structure grid codes––Zeus TLNS3D/CFL3D, OVERFLOW
Navier–Stokes technology using structured grids was well developed by the early 1990s and is available to the industry. However, most existing structured grid Navier–Stokes codes require the users to provide high-quality 3D grids to resolve detailed viscous flows near configuration surfaces and viscous wake regions. The task of grid generation––both surface grid and field grid––has become one of the essential elements, as well as the bottleneck in using Navier–Stokes technology for complex configuration/complex flow analysis. In addition, most Navier–Stokes solvers have not been thoroughly checked out and validated for numerical accuracy, convergence reliability, and application limitations. Boeing has acquired several Navier–Stokes codes from NASA, as well from other research organizations, and has devoted a great deal of effort testing the codes and validating numerical results with available wind tunnel and flight data. In addition, to make the codes usable tools for engineering design, Boeing CFD developers have rewritten a 3D grid generation code through the use of an advancing front approach [50], so that a precise control on grid quality, such as grid spacing, stretching ratio, and grid orthogonality near configuration surfaces can be achieved. This is an important requirement for accurate resolution of viscous flow regions for all existing Navier–Stokes solvers. Two structured grid generation approaches are currently in use (i.e., the matched/patched multiblock grid approach and the overset or overlap grid approach). The former approach subdivides the flowfield into a number of topologically simple regions, such that in each region high quality grid can be generated. This is a rather time-consuming and tedious process for complex configuration analysis. However, once this ‘‘blocking’’ process is done for one configuration, a similar configuration can be done easily through the use of script or command files. The TLNS3D/CFL3D based Zeus Navier–Stokes analysis system [51] developed and used at Boeing for Loads and Stability and Control applications belongs to this structured, multiblock grid approach. The Zeus analysis system inherited the process developed in the A488 system, which packaged many user-friendly preprocessing programs that handled geometry and flow condition input as well as postprocessing programs that printed and plotted wing sectional data and airplane force and moment data. This has allowed the design engineers to reduce their input to just geometry lofts and flight conditions and obtain the solution within a few hours or overnight depending on the size of the problem and the availability of the computing resources. The Zeus system is illustrated in Fig. 18.
Some recent applications of using the Zeus Navier–Stokes analysis system include the prediction of Reynolds number effects on tail effectiveness, shown in Fig. 19. CFD results captured the effect of Reynolds number on horizontal tail boundary layer health and on tail effectiveness quite well.
Another application is the simulation of vortex generators on a complete airplane configuration [52] as shown in Fig. 20. The effects of vortex generators on airplane pitch characteristics are shown. Again, the results compare reasonably well with flight data with respect to predicting airplane pitch characteristics, even at relatively high angles of attack where the flow is massively separated. The CFD solution also provides flowfield details that illustrate the flow physics behind how vortex generators work to improve high-speed handling characteristics, a very useful tool for design engineers in selecting and placing vortex generators on lifting surfaces.
The second structured grid Navier–Stokes method uses the overset grid approach, whereby the flowfield grid is generated for each component of the configuration independently. Each set of grid overlaps with other set or sets of grid, and communication between various sets of grid is achieved through numerical interpolation in the overlap region. The advantage of this approach is that each component of the configuration is relatively simple, and a high-quality local grid can be easily generated. However, one pays the price of performing complex 3D interpolation with some risk of degrading overall numerical accuracy. The OVERFLOW code [43] used at Boeing for high-speed and high-lift configuration analysis belongs to this overset/overlap structured grid approach. Fig. 21 shows the overset grids and OVERFLOW solution of a complex high-lift system, including all high-lift components of the airplane [53]. Results agree well with experimental data for low to moderate angle of attacks. At high angle of attack, there are complex flow separations in the flap and slat gap regions, which could not be simulated adequately with the current one- or two-equation turbulence models. Improvements in turbulence models for separated flow simulation, as well as Navier–Stokes solver accuracy and robustness, are essential for a reliable prediction of airplane high-lift performance, as well as airplane pitch characteristics.
Another important element for successful use of Navier–Stokes technology in airplane design and analysis is the availability of high-performance computing. All Navier–Stokes codes require large memory and many CPU hours to resolve viscous flows over an airplane configuration. The rapid development of parallel computing hardware and software, as well as PC clusters with large number of CPUs, have made the use of Navier–Stokes technology in practical airplane design and analysis a reality. The analysis of an airplane configuration with 16 vortex generators on each side of the wing consists of approximately 25 million points. Using 56 CPUs on a SGI Origin 2000 machine, the CFD solution for each flight condition can be obtained within 11 h of flow time.
4.4.2. Unstructured grid codes––Fluent, NSU2D/3D, CFD++
The structured grid Navier–Stokes codes make highly efficient use of computer memory and processing power due to the well-ordered data structure used in the solution algorithm. However, they suffer two major drawbacks; i.e., the lack of flexibility in handling complex geometry and the difficulty of implementing solution adaptive gridding. These requirements, namely, complex geometry and solution adaptive capability, are essential for accurate and reliable predictions of airplane design and off-design performance. Consequently, it is less common and often more difficult to use CFD to analyze geometrically complex parts of the airplane, such as high-lift systems (flaps and slats), engine compartments, auxiliary power units, and so on. Paradoxically, the success of CFD in designing major components has eliminated many of the experiments that previously provided a ‘‘piggyback’’ opportunity to test these complicated devices. Consequently, there is an increased need to compute airflows around and through systems that are distinguished by very complex geometry and flow patterns. In the last decade, there has been impressive progress in unstructured grid Navier–Stokes code developments [54–57]. Boeing Commercial Airplanes has explored and used Fluent, the most recent unstructured grid Navier–Stokes codes NSU2D/NSU3D of Mavriplis [54], and CFD++ of Chakravarthy [57] for 2D and 3D high-lift analysis with success.
A recent application of unstructured grid technology involved the use of Fluent V5 [58] to investigate the behavior of the efflux from engine thrust reversers [59]. A typical commercial airplane deploys its thrust reversers briefly after touch down. A piece of engine cowling translates aft and blocker doors drop down, directing the engine airflow into a honeycomb structure called a cascade. The cascade directs the flow forward, which acts to slow the aircraft and decrease lift for more effective braking. There are some critical design considerations in properly directing the reversed flow. The reverser is used precisely at the time when high-lift devices, wing leading and trailing edge flaps and slats, are fully deployed. Consequently, the plumes of hot exhaust must be directed so as not to impinge on these devices. In addition, the plumes should not hit the fuselage or other parts of the aircraft. Moreover, reingestion (in which the reversed plume reenters the engine inlet), engine ingestion of debris blown up from the runway, and plume envelopment of the vertical tail (which affects directional control) must be avoided. To eliminate these effects, it's important for designers to know exactly where the exhaust plumes go.
The Tetra module of grid generation software from ICEM CFD Engineering [60] has been used to obtain fully unstructured meshes. Starting from a new airplane geometry (with cleaned up lofts), these meshes can be created in a day or two. The grid generation software contains a replay capability so that minor changes to the geometry can be remeshed quickly. Because the entire CFD analysis cycle can be completed in about three days, designers can use this tool repeatedly as a way to optimize the design. In this way, it is possible to map the performance of the reverser against the power setting of the reversed engine fan and the airplane forward speed. Tests that involve geometry changes, such as the repositioning of the cascades or the nacelle relative to the wing or variation of the cascade angles, can be accomplished with minimal remeshing and analysis. Wind tunnel testing and expense are reduced, but the key benefits are really time and risk mitigation. If a need to change the design should become apparent after the tooling was built and aircraft was in test, the delay in entry into service and the expense of retooling would be unacceptable. The grid and engine reverser efflux particle traces from one of these cases is illustrated in Fig. 22. Fluent is in widespread use at Boeing for other geometrically complex problems, such as cooling flows in engine compartments and dispersion of fire suppression chemicals.
4.4.3. Other Navier–Stokes codes
The Propulsion Analysis group at Boeing Commercial Airplanes has long acquired, supported, and used a number of other Navier–Stokes codes. The present authors are not qualified to describe this activity; however, we do wish to mention some of the codes involved. These include the Boeing named Mach3 code based on the implicit predictor, corrector methodology of McCormack [61], the PARC code [62] of NASA Lewis, the WIND code [63], and BCFD [64], which is scheduled to be the platform for an Enterprise common Navier–Stokes code. These codes have been used for nacelle inlet analysis and design and for nacelle fan and core cowl nozzle performance studies [64,65].
4.4.4. Next generation Navier–Stokes codes
The successful application of Navier–Stokes codes during the last 10 years has raised expectations among Boeing engineers that CFD can become a routine tool for the loads analysis,stability and control analysis, and high-lift design processes. In fact, there is considerable speculation that it may be possible to populate databases involving tens of thousands of cases with results from Navier–Stokes CFD codes, if dramatic improvements in computing affordability continue over the next five years. For the first time, the affordability per Navier–Stokes data point may rival that of a wind tunnel generated data point. Of course, project engineers use CFD and wind tunnel data in a complementary fashion so that cost is not a competitive issue here. Before Navier–Stokes codes can be routinely used to populate databases; however, accuracy, reliability, efficiency, and usability issues need to be addressed. Gaps in data, inconsistent data, and long acquisition times seriously degrade the utility of a database. Even with current user aids, the application of Navier–Stokes codes to new configurations generally requires the services of an expert user. The generation of a ‘‘good grid’’ is still somewhat of an art and often quite labor intensive. Although everyone realizes that a ‘‘good grid’’ is necessary for accuracy and even convergence, there is no precise definition of what constitutes a ‘‘good grid’’. In fact, the definition would probably vary from code to code and is certainly case dependent. Usability problems are reflected in the fact that although Navier–Stokes codes are now considered capable of generating more accurate results, they are used far less frequently than TRANAIR at Boeing Commercial Airplanes.
Much of the current effort to improve the usability of our Navier–Stokes codes would have to be termed evolutionary. As is always the case with evolutionary improvements, it is necessary to determine whether or not incremental improvements are approaching a horizontal asymptote, while implementation costs are mounting. Boeing is currently involved in an effort to reevaluate the current technology and explore alternatives, much the same as was done 20 years ago in the case of potential flow. The project is called General Geometry Navier–Stokes Solver (GGNS).
From our TRANAIR experience, it seems rather evident that solution adaptive grids must be an essential feature for reliability and usability. This is especially true when computing flows at off-design conditions where our understanding of the flow physics is limited, making it difficult to generate ‘‘good grids’’. However, these grids must now be anisotropic and, more than likely, quite irregular. This places a huge burden on improving discretization fidelity, as current discretization algorithms do not seem to do well with irregular spacings and cell shapes. Higher order elements are certainly desirable for efficiency's sake and for capturing latent features. However, stabilization and limiter technologies need to be advanced to handle such elements. Current solvers are relatively weak, and convergence is often incomplete, especially when turbulent transport equations are involved. Some of these issues are addressed in detail elsewhere [66]. It should be noted that our reevaluation and development work here is a joint effort between the CFD developers at Boeing and their colleagues at the Boeing Technical Research Center in Moscow. We also note there are related efforts going on elsewhere. We mention in particular the FAAST project at NASA Langley.
4.5. Design and optimization methods
4.5.1. A555, A619 inverse design codes
Most existing CFD codes are analysis tools (i.e., given a configuration, the codes predict aerodynamic characteristics of the configuration). In airplane design, one would like to have tools that can provide design capability (i.e., given airplane aerodynamic characteristics, the codes generate realistic geometry). The design method used by Henne [67], which prescribes wing surface pressures and employs an iterative method to find the corresponding geometry, was one of the very first inverse design methods used in the airplane industry. Boeing Commercial Airplanes developed a similar method for wing design using the A555 code [68], illustrated in Fig. 23. This code was used extensively on the 7J7, 777, and 737NG programs. The code borrowed heavily from the A488 system to ensure usability in the fast-paced airplane development environment. On the Boeing 777 program, CFD contributed to a high degree of confidence in performance with only a three-cycle wing development program. Significantly fewer wing designs were tested for the 777 than for the earlier 757 and 767 programs. The resulting final design would have been 21% thinner without the ‘‘inverse design’’ CFD capability of A555. Such a wing would not have been manufacturable due to skin gages being too thick for the automatic riveting machines in the factory, and it would have less fuel volume. Conversely, if the wing could meet the skin gage and fuel volume requirements, the cruise Mach number would have had to be significantly slower. In either case, the airplane would not have achieved customer satisfaction. The effect of CFD wing design in this case was an airplane that has dominated sales in its class since being offered to the airlines.
More recently, Campbell [69] introduced a constrained, direct, iterative, surface curvature method (CDISC) for wing design. The method has been incorporated into both the structured grid single-block Navier–Stokes code A619 [70], and the overset grid code OVERFLOW/OVERDISC at Boeing. Both codes are in use for configuration design in the product development organization.
4.5.2. TRANAIR optimization
Because of boundary condition generality, and in particular the use of transpiration to simulate surface movement, the TRANAIR code could have easily been substituted into the existing Boeing standard inverse aerodynamic design process, A555. However, the process itself had a number of issues. First and foremost was the difficulty of finding ‘‘good’’ pressure distributions for highly 3D flows. Such pressure distributions needed to result in acceptable off-design performance as well as low cruise drags. Although many rules of thumb were developed through the years, only a few highly experienced aerodynamicists could create acceptable distributions on a routine basis. Second, it was never clear whether the resultant designs were in fact optimal, a question of some importance in a highly competitive environment. Third, multidisciplinary constraints often had to be imposed after the fact leading to a highly iterative and time consuming process as well as potentially suboptimal designs.
A serendipitous result of the decision to use a powerful sparse solver to converge the TRANAIR analysis cases was the ability to rapidly generate solution sensitivities. In a sense, each sensitivity represented just another right hand side for the already decomposed analysis Jacobian matrix to solve. In addition, the adaptive grid capability allowed accurate tracking of changes in critical flow features predicted by these sensitivities. Formally, it was an easy matter to feed the sensitivities into an optimization driver such as NPSOL [71] and systematize the design process as illustrated in Fig. 24. However, optimization codes have been notorious for promising spectacular results and then falling flat because of overly simplistic mathematical realizations of the problems. Aerodynamic design requires understanding of very complicated geometric, flow and interdisciplinary constraints. These constraints are rather nebulous and often exist only in the minds of the designers. An initial optimization capability using TRANAIR was available in 1992 [72], but it took several more years before project users were willing to trust their design processes to optimization [73]. A wide variety of payoff functions and constraints were built into TRANAIR, but the one component of a payoff function that users were really interested in was, of course, drag. Consequently, a great deal of effort was invested in numerical work to improve TRANAIR's drag calculations. Careful studies in the mid-1990s [74] then validated the ability of TRANAIR to compute accurate drag increments for subsonic transports.
At the same time, a multipoint optimization capability was introduced, since it was well understood that drag minimization at a single flight condition was somewhat ill-posed and often led to unacceptable off design characteristics. Moreover, users desired capability for simultaneously optimizing slightly different configurations having major portions of their geometries in common. By 1997, TRANAIR optimization had replaced inverse design as the preferred aerodynamic design process for flight conditions where full potential/boundary layer modeling is applicable. At the current time, the code can handle as many as 600 geometry degrees of freedom and 45,000 nonlinear inequalities. These inequalities represent the pointwise application of roughly 25 different types of flow and geometry constraints. The code has seen extensive use in the design of a large variety of configurations covering the Mach range from transonic to Mach 2.4. This has contributed (in several cases critically) to detailed development studies for a number of vehicles, some of which are illustrated in Fig. 25.
TRANAIR design/optimization applications that have affected a product include the payload fairing on the Sea Launch rocket, nacelle fan cowl for the GE90-115B engine, and the process used to determine ‘‘Reduced Vertical Separation Minimums’’ compliance for new and in-service aircraft.
Conclusions
During the last 30 years at Boeing Commercial Airplanes, Seattle, CFD has evolved into a highly valued tool for the design, analysis, and support of cost-effective and high-performing commercial transports. The application of CFD today has revolutionized the process of aerodynamic design, and CFD has joined the wind tunnel and flight test as a critical tool of the trade. This did not have to be the case; CFD could have easily remained a somewhat interesting tool with modest value in the hands of an expert as a means to assess problems arising from time to time. As the reader can gather from the previous sections, there are many reasons that this did not happen. The one we would like to emphasize in this Conclusion section is the fact that Boeing recognized the leverage in getting CFD into the hands of the project engineers and was willing to do all the things necessary to make it happen.
n5321 | 2025年7月29日 20:58